
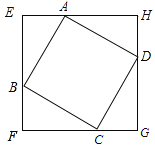
【题目】如图,正方形ABCD的边长为8cm,分别过四个顶点A、B、C、D做四条直线EF、FG、GH、HE,并保证相邻两条直线垂直,相交于E、F、G、H四点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)判断无论如何按照上述要求作图,线段EG、AC的中点是否重合,并说明理由;
(3)判断四边形EFGH的面积有无最大值,若有请写出面积最大值,并说明理由.
【答案】(1)证明见解析;(2)线段EG、AC的中点重合,理由见解析;(3)面积最大值为128cm2,理由见解析.
【解析】试题分析:(1)由正方形的性质得出∠BAD=∠B=∠BCD=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;(2)连接AC、EG,交点为O;先证明△AOE≌△COG,得出OA=OC,证出O为对角线AC、BD的交点,即O为正方形的中心;(3)理由叙述合理即可.
(1)∵相邻两条边互相垂直,
∴∠E=∠F=∠G=∠H=90°,
又∵AE=BF=CG=DH,AB=BC=CD=DA,
∴△EAB≌△FBC≌△GCD≌△HAD,
∴AH=BE=CF=DG,
∴EF=FG=GH=HE,
∵相邻两条边互相垂直,
∴四边形EFGH是正方形;
(2)(证法不唯一)
线段EG、AC的中点重合.
连结EC、AG,
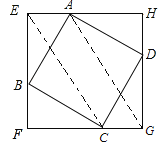
∵AE= CG,且AE∥CG,
∴四边形AECG为平行四边形,
∴线段EG、AC的中点重合.
(3)有最大值,面积最大值为128cm2.如图,
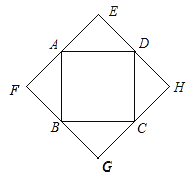
当ABCD分别为各边中点时,四边形EFGH面积最大.(理由叙述合理即可.)
例如:在各种情况中当ABCD分别为各边中点时,四边形EFGH边长为正方形ABCD对角线,其他情况中边长都比对角线小.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下列命题中不成立的是( )
A.矩形的对角线相等
B.三边对应相等的两个三角形全等
C.两个相似三角形面积的比等于其相似比的平方
D.一组对边平行,另一组对边相等的四边形一定是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省泰安市第22题)如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点2015年六月份共接待游客25万人次,八月份共接待游客64万人次,设六至八月每月游客人次的平均增长率为x,则可列方程为( )
A.25(1+x)2=64
B.25(1﹣x)2=64
C.64(1+x)2=25
D.64(1﹣x)2=25
查看答案和解析>>
科目:初中数学 来源: 题型:
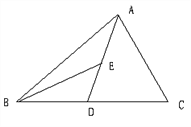
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com