
【题目】如图,△ABC中,AB=BC=5cm,AC=6cm,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,BP长度为ycm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:
(1)通过取点,画图,测量,得到了x(秒)与y(cm)的几组对应值:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.5 | 4.1 | 4 | 4.5 | 5.0 |
要求:补全表格中相关数值(保留一位小数);
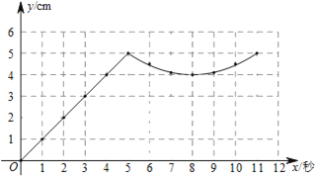
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当x约为______时,BP=CP.
【答案】(1)见解析,5.0;4.1;(2)见解析;(3)2.5或9.1
【解析】
(1)根据点P在第5秒与第9秒的位置,分别求出BP的长,即可得到答案;
(2)根据表格中的x,y的对应值,描点、连线,画出函数图象,即可;
(3)令CP=y′,确定P在BC和AC上时,得y′=-x+5 或y′=x-5,画出图象,得到图象的交点的横坐标,即可求解.
(1)当x=5时,点P与点C重合,y=5,
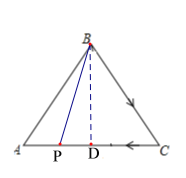
当x=9时,点P在AC边上,且CP=9×1-5=4cm,
过点B作BD⊥AC于点D,则CD=![]() AC=3cm,BD=
AC=3cm,BD=![]() cm,
cm,
∴DP=CP-CD=4-3=1cm,BP=![]() cm,即:y=4.1.
cm,即:y=4.1.
如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 4.5 | 4.1 | 4.0 | 4.1 | 4.5 | 5.0 |
故答案为:5.0;4.1;
(2)描点、连线,画出函数图象如下:
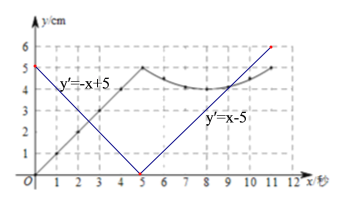
(3)令CP=y′,
当0≤x≤5时, y′=-x+5;
当5<x≤11时,y′=x-5,
画出图象可得:当x=2.5或9.1时,BP=PC.
故答案为:2.5或9.1.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是以
是以![]() 为直径的
为直径的![]() 上的一点,
上的一点,![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线,与
的切线,与![]() 的延长线相交于点
的延长线相交于点![]() ,点
,点![]() 是
是![]() 的中点,连结
的中点,连结![]() 交
交![]() 于点
于点![]()

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() 的半径长为
的半径长为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
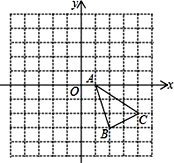
【题目】如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(2,-3),C(4,-2).
(1)在图中作出△ABC关于x轴对称的图形△A1B1C1.
(2)作出△A1B1C1向左平移4个单位长度后得到的△A2B2C2,并直接写出点C2的坐标_____.
(3)△A2B2C2的面积是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
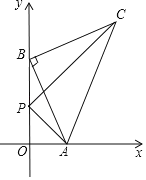
【题目】如图,在平面直角坐标系中,等腰直角△ABC,AB⊥BC,AB=BC,点C在第一象限.已知点A(m,0),B(0,n)(n>m>0),点P在线段OB上,且OP=OA.
(1)点C的坐标为 (用含m,n的式子表示)
(2)求证:CP⊥AP.
查看答案和解析>>
科目:初中数学 来源: 题型:
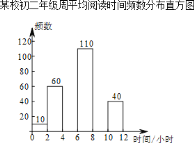
【题目】《北京中小学语文学科教学21条改进意见》中的第三条指出:“在教学中重视对国学经典文化的学习,重视历史文化的熏陶,加强与革命传统教育的结合,使学生了解中华文化的悠久历史,增强民族文化自信和价值观自信,使语文教学成为涵养社会主义核心价值观的重要源泉之一”.为此,昌平区掀起了以“阅读经典作品,提升思维品质”为主题的读书活动热潮,在一个月的活动中随机调查了某校初二年级学生的周人均阅读时间的情况,整理并绘制了如下的统计图表:
某校初二年级学生周人均阅读时间频数分布表
周人均阅读时间x (小时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | 0.275 |
8≤x<10 | 100 | 0.250 |
10≤x<12 | 40 | b |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题:
(1)在频数分布表中a=______,b=______;
(2)补全频数分布直方图;
(3)若该校有1600名学生,根据调查数据请你估计,该校学生周人均阅读时间不少于6小时的学生大约有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
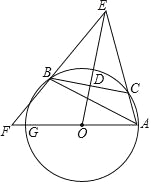
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
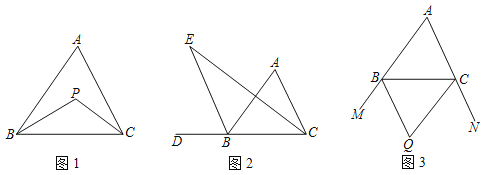
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC= ;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°![]() ∠A
∠A
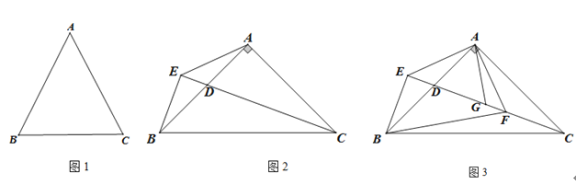
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com