
【题目】李克强总理说:”一个国家养成全民阅读习惯非常重要…我希望全民阅读能够形成一种氛围,无处不在.“为了响应国家的号召,某”希望“学校的全体师生掀起了阅读的热潮.下面是该校三个年级的学生人数分布扇形统计图与学生在4月份阅读课外书籍人次的统计图表,其中七年级的学生人数为240人.请解答下列问题:
图书种类 | 频数 | 频率 |
科普书籍 | A | B |
文学 | 1200 | C |
漫画丛书 | D | 0.35 |
其他 | 200 | 0.05 |
(1)该校七年级学生人数所在扇形的圆心角为______°,该校的学生总人数为______人;
(2)请补全条形统计图;
(3)为了鼓励学生读书,学校决定在“五四”青年节举行两场读书报告会.报告会的内容从“科普书籍”“文学”“漫画丛书”“其他”中任选两个.用画树状图或列表的方法求两场报告会的内容恰好是“科普书籍”与“漫画丛书”的概率.(“科普书籍”“文学”“漫画丛书”“其他”,可以分别用K,W,M,Q来表示)

【答案】108800
【解析】
(1)由八年级和九年级学生所占比例可知七年级学生所占比例,用360°乘以七年级所占比例即可求得扇形圆心角度数,用七年级人数除以其所占百分比即可得该校学生总数,
(2)由“其他”的频数及其频率求得书籍总数,再用总数乘以“漫画丛书”的频率求得其频数,用总数量减去其它三类书籍的总数即可得科普书籍数量,
(3)画出树状图就可以将所有情况全部列举出来,求得恰好是“科普书籍”与“漫画丛书”的概率即可
(1)该校七年级学生人数所在扇形的圆心角为360°×(1﹣30%﹣40%)=108°,该校学生总人数为240÷(1﹣30%﹣40%)=800(人),
故答案为:108、800;
(2)书籍总数为200÷0.05=4000,
则漫画丛书为4000×0.35=1400,科普书籍为4000﹣(1200+1400+200)=1200,
补全条形图如下:

(3)画树状图如下:

由树状图知,共有12种等可能结果,其中符合条件的结果有2种,
所以两场报告会的内容恰好是“科普书籍”与“漫画丛书”的概率为![]() ,
,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
求证:AD平分∠BAC,填写分析和证明中的空白.

证明:∵AD⊥BC,EF⊥BC(已知)
∴______∥______(______)
∴______=______(两直线平行,内错角相等)
______=______(两直线平行,同位角相等)
∵______(已知),∴______
即AD平分∠BAC(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,则:
,则:
①线段PB= ,PC= ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足![]() ,求
,求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )

A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线![]() 上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线
上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() 与直线l的交点即为P,且PA+PB的最小值为
与直线l的交点即为P,且PA+PB的最小值为![]() .
.


请利用上述模型解决下列问题:
(1)几何应用:如图2,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
(2)代数应用:求代数式![]() +
+![]() (0≤x≤3)的最小值.
(0≤x≤3)的最小值.
(3)几何拓展:如图3,△ABC中,AC=2,∠A=30°,若在AB、AC上各取一点M、N使BM+MN的值最小,最小值是 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
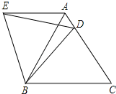
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.
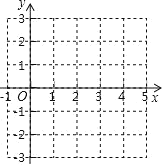
(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
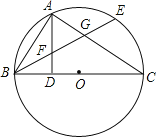
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com