
【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=![]() BC,②
BC,②![]() ,③
,③![]() AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
∵Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,
∴AD =DC,∠EAD=∠C=450,∠EDA=∠MDN-∠ADN =900-∠AND=∠FDC。
∴△EDA≌△FDC(ASA)。∴AE=CF。∴BE+CF=" BE+" AE=AB。
在Rt△ABC中,根据勾股定理,得AB=![]() BC。∴(BE+CF)=
BC。∴(BE+CF)=![]() BC。∴结论①正确。
BC。∴结论①正确。
设AB=AC=a,AE=b,则AF="BE=" a-b。
∴![]() 。
。
∴![]() 。∴结论②正确。
。∴结论②正确。
如图,过点E作EI⊥AD于点I,过点F作FG⊥AD于点G,过点F作FH⊥BC于点H,ADEF相交于点O。

∵四边形GDHF是矩形,△AEI和△AGF是等腰直角三角形,
∴EO≥EI(EF⊥AD时取等于)=FH=GD,
OF≥GH(EF⊥AD时取等于)=AG。
∴EF=EO+OF≥GD+AG=AD。∴结论④错误。
∵△EDA≌△FDC,
∴![]() 。∴结论③错误。
。∴结论③错误。
又当EF是Rt△ABC中位线时,根据三角形中位线定理知AD与EF互相平分。
∴结论⑤正确。
综上所述,结论①②⑤正确。故选C。


科目:初中数学 来源: 题型:
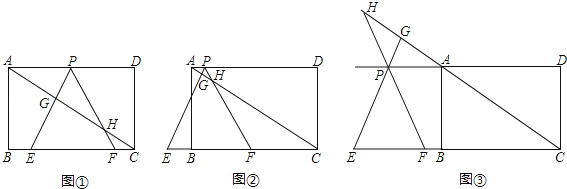
【题目】如图①,在矩形ABCD中,AB=![]() ,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.
,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.
(1)求△PEF的边长;
(2)若△PEF的边EF在线段CB上移动,试猜想:PH与BE有何数量关系?并证明你猜想的结论;
(3)若△PEF的边EF在射线CB上移动(分别如图②和图③所示,CF>1,P不与A重合),(2)中的结论还成立吗?若不成立,直接写出你发现的新结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
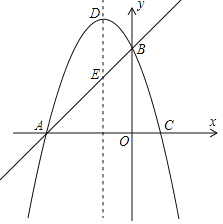
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
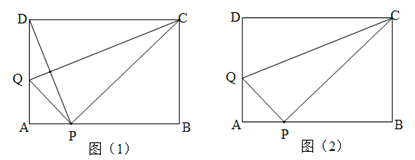
【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
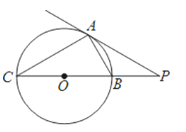
【题目】如图,点P是⊙O外一点,过点P作⊙O的切线,切点为A,连接PO并延长,交⊙O于B、C两点.
(1)求证:△PBA∽△PAC;
(2)若∠BAP=30°,PB=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
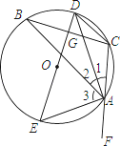
【题目】如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
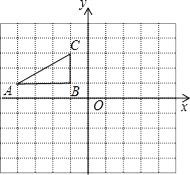
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1,并写出A1的坐标;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程以及Rt△A1B1C1扫过的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
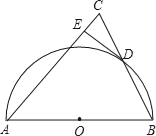
【题目】如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,连接AC,过点D作DE⊥AC于点E.
(1)请猜想DE与⊙O的位置关系,并说明理由;
(2)当AB=4,∠BAC=45°时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com