
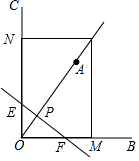
 ��ͼ����BOC=90�㣬��A�ڡ�BOC���ڲ���OA=2����AOC=30�㣬��P��Q�ֱ�ӵ�O��Aͬʱ����������ÿ��1����λ���ȵ��ٶ���OA�����˶�������P��ֱ��l��OA��P������Q��QM��OB�ڵ�M��QN��OC�ڵ�N�����P�˶�ʱ��Ϊt��s��
��ͼ����BOC=90�㣬��A�ڡ�BOC���ڲ���OA=2����AOC=30�㣬��P��Q�ֱ�ӵ�O��Aͬʱ����������ÿ��1����λ���ȵ��ٶ���OA�����˶�������P��ֱ��l��OA��P������Q��QM��OB�ڵ�M��QN��OC�ڵ�N�����P�˶�ʱ��Ϊt��s������ ��1��������OQ=OA+AQ=2+t��PO=t�������Ƴ�PQ=OQ-OP=��2+t��-t=2��
��2������ͼ1�У�����N���F�غ�ʱ����Rt��PQN�У��ɡ�PQN=30�㣬PQ=2���Ƴ�PN=PQ•tan30��=$\frac{2}{3}$$\sqrt{3}$����Rt��OPN�У�OP=PN•tan30��=$\frac{2}{3}$���ɴ˼������t��ֵ��
����ͼ2�У�����M���E�غ�ʱ����Rt��PQM�У��ɡ�PMQ=30�㣬PQ=2���Ƴ�PM=$\frac{PQ}{tan30��}$=2$\sqrt{3}$����Rt��OPM�У�OP=$\frac{PM}{tan30��}$=6���ɴ˼����t��ֵ��
��3���������������ۢ���ͼ3�У���0��t��$\frac{2}{3}$ʱ��ֱ��lɨ������QMON��ͼ���ǡ�OMN������ͼ4�У�$\frac{2}{3}$��t��6ʱ��ֱ��lɨ������QMON��ͼ�����ı���MOFK������ͼ5�У���t��6ʱ��ֱ��lɨ������QMON��ͼ���������EOFKG���ֱ���⼴�ɣ�
��4��������������ͼ6�У���AF��ONʱ������ͼ7�У���AE��OMʱ���ֱ����OP�ij����ɽ�����⣮
��� �⣺��1��������OQ=OA+AQ=2+t��PO=t��
��PQ=OQ-OP=��2+t��-t=2��
��OQ=2+t��PQ=2��
��2������ͼ1�У�����N���F�غ�ʱ��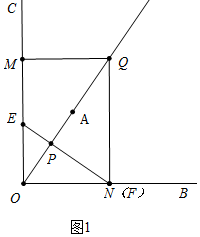
��Rt��PQN�У��ߡ�PQN=30�㣬PQ=2��
��PN=PQ•tan30��=$\frac{2}{3}$$\sqrt{3}$��
��Rt��OPN�У�OP=PN•tan30��=$\frac{2}{3}$����ʱt=$\frac{2}{3}$s��
����ͼ2�У�����M���E�غ�ʱ��
��Rt��PQM�У��ߡ�PMQ=30�㣬PQ=2��
��PM=$\frac{PQ}{tan30��}$=2$\sqrt{3}$��
��Rt��OPM��OP=$\frac{PM}{tan30��}$=6��
��ʱt=6s��
��3������ͼ3�У���0��t��$\frac{2}{3}$ʱ��ֱ��lɨ������QMON��ͼ���ǡ�OMN����֪ON=2t��OM=$\frac{2}{3}$$\sqrt{3}$t��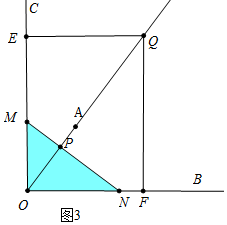
��S=$\frac{1}{2}$•ON•OM=$\frac{2}{3}$$\sqrt{3}$t2��
����ͼ4�У�$\frac{2}{3}$��t��6ʱ��ֱ��lɨ������QMON��ͼ�����ı���MOFK��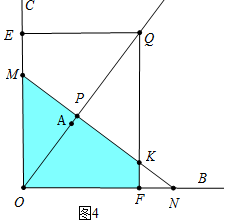
S=S��OMN-S��FKN=$\frac{2}{3}$$\sqrt{3}$t2-$\frac{1}{2}$•��2t-$\frac{t+2}{2}$��•$\frac{\sqrt{3}}{3}$��2t-$\frac{t+2}{2}$��=$\frac{7\sqrt{3}}{24}$t2+$\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{6}$��
����ͼ5�У���t��6ʱ��ֱ��lɨ������QMON��ͼ���������EOFKG��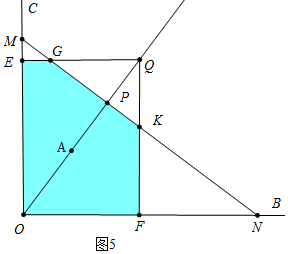
S=S��OMN-S��KFN-S��EGM=$\frac{7\sqrt{3}}{24}$t2+$\frac{\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{6}$-$\frac{1}{2}$•[$\frac{2\sqrt{3}}{3}$t-��t+2��•$\frac{\sqrt{3}}{2}$]•$\sqrt{3}$•[$\frac{2\sqrt{3}}{3}$t-��t+2��•$\frac{\sqrt{3}}{2}$]=$\frac{\sqrt{3}}{4}$t2+$\sqrt{3}$t-$\frac{5\sqrt{3}}{3}$��
����������S=$\left\{\begin{array}{l}{\frac{2\sqrt{3}}{3}{t}^{2}}&{��0��t��\frac{2}{3}��}\\{\frac{7\sqrt{3}}{24}{t}^{2}+\frac{\sqrt{3}}{2}t-\frac{\sqrt{3}}{6}}&{��\frac{2}{3}��t��6��}\\{\frac{\sqrt{3}}{4}{t}^{2}+\sqrt{3}t-\frac{5\sqrt{3}}{3}}&{��t��6��}\end{array}\right.$
��4������ͼ6�У���AF��ONʱ��
��Rt��OAF�У�OF=OA•cos60��=1��
��Rt��OPF�У�OP=$\frac{1}{2}$OF=$\frac{1}{2}$����ʱt=$\frac{1}{2}$s��
����ͼ7�У���AE��OMʱ��
��Rt��AEO�У�OE=OA•cos30��=$\sqrt{3}$��
��Rt��OPE�У�OP=OE•cos30��=$\frac{3}{2}$��
������������tΪ$\frac{1}{2}$s��$\frac{3}{2}$sʱ��ֱ��AE��ֱ��AF������ֱ�ߵ�һ�������QMON�ıߴ�ֱ��
���� ���⿼���ı����ۺ��⡢���ε����ʡ�������Ǻ����������ε�����Լ�·�̡��ٶȡ�ʱ��֮��Ĺ�ϵ��֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬ѧ�����÷ָ�����ε�����������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ������ֱ�ǡ�ABC�����ֱ�ǡ�CEF����ABC=��CEF=90�㣬����AF��MʱAF���е㣬����MB���ҵ�C��B��E��ͬһֱ���ϣ���֤��BM��CF��
��֪����ͼ������ֱ�ǡ�ABC�����ֱ�ǡ�CEF����ABC=��CEF=90�㣬����AF��MʱAF���е㣬����MB���ҵ�C��B��E��ͬһֱ���ϣ���֤��BM��CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | -2 | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
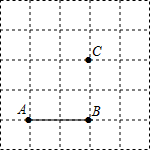 ��ͼ����֪�߶�AB����C���ڷ���ֽ�ϻ�ͼ���ش����⣮
��ͼ����֪�߶�AB����C���ڷ���ֽ�ϻ�ͼ���ش����⣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com