
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.

【答案】(1)见解析;(2)证明见解析;(3)存在,作图见解析;点![]() 到
到![]() 三点的距离之和最小值为
三点的距离之和最小值为![]() 米.
米.
【解析】
(1)根据垂线段最短、利用尺规作图作出点P;
(2)将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,根据作图可知
,根据作图可知![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() ,根据两点之间线段最短可知,当
,根据两点之间线段最短可知,当![]() 时,
时,![]() 短,
短,
(3)以BC为边作正△BCD,使点D与点A在BC两侧,作△BCD的外接圆,连接AD交圆于P,连接PB,作DE⊥AC交AC的延长线于E,根据勾股定理、直角三角形的性质计算,得到答案.
解:(1)如图①,过点![]() 作
作![]() 的垂线,
的垂线,
垂足为![]() ,点
,点![]() 记为所求;
记为所求;
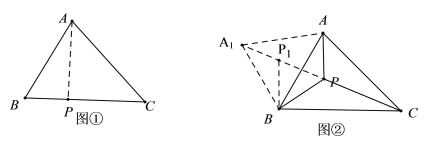
(2)如图②,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,
,
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,
,
连接![]() ,
,![]() ,
,![]() ,
,
根据作图可知![]() 和
和![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
连接![]() ,根据两点之间线段最短可知,
,根据两点之间线段最短可知,
当![]() 时,
时,
![]() 最短,
最短,
∵![]() ,
,
∴![]() ,
,
又∵![]() 为等边三角形,
为等边三角形,
![]()
∴![]() 四点共线,
四点共线,
∴![]() ,
,
∴当![]() 时,
时,![]() 最短;
最短;
(3)存在符合条件的点![]() .
.
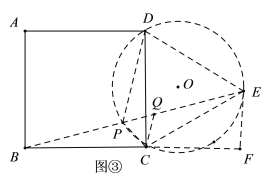
如解图③,以![]() 为作等边
为作等边![]() ,在作
,在作![]() 的外接圆
的外接圆![]() ,
,
连接![]() ,交
,交![]() 于点
于点![]() ,
,
此时![]() 最小,
最小,
在![]() 上截取
上截取![]() .
.
∵在等边![]() 中,
中,
![]()
∴![]() (同弧所对的圆周角相等)
(同弧所对的圆周角相等)
∴![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 最小.
最小.
理由如下:
设点![]() 为正方形
为正方形![]() 内任意一点,
内任意一点,
连接![]() ,
,![]() 、
、![]() ,
,
将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() .
.
∵![]() ,
,
∴![]() 为
为![]() 的最短距离.
的最短距离.
在![]() 中,
中,![]() ,
,![]() 米,
米,
∴![]() (米),
(米),
![]() (米),
(米),
∴![]() (米).
(米).
在![]() 中,
中,![]()
![]() .
.
∴点![]() 到
到![]() 三点的距离之和最小值为
三点的距离之和最小值为![]() 米.
米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标是(-1,0),点
的坐标是(-1,0),点![]() 的坐标是(0,6),
的坐标是(0,6),![]() 为
为![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 逆时针旋转90°.后得到
逆时针旋转90°.后得到![]() .若反比例函数
.若反比例函数![]() 的图像恰好经过
的图像恰好经过![]() 的中点
的中点![]() ,则k的值是( )
,则k的值是( )
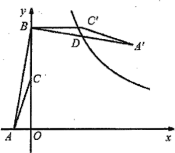
A.19B.16.5C.14D.11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
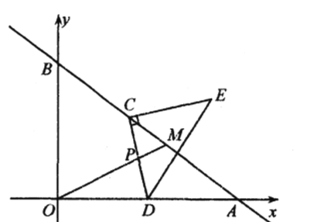
【题目】如图,在平面直角坐标系中,直线分![]() 别交
别交![]() 轴、
轴、![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .动点
.动点![]() 在直线
在直线![]() 上以每秒
上以每秒![]() 个单位的速度从点
个单位的速度从点![]() 向终点
向终点![]() 运动,同时,动点
运动,同时,动点![]() 以每秒
以每秒![]() 个单位的速度从点
个单位的速度从点![]() 沿
沿![]() 的方向运动,当点
的方向运动,当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 同时停止运动.设运动时间为
同时停止运动.设运动时间为![]() 秒.
秒.
(1)求点![]() 的坐标和
的坐标和![]() 的长.
的长.
(2)当![]() 时,线段
时,线段![]() 交
交![]() 于点
于点![]() 且
且![]() 求
求![]() 的值.
的值.
(3)在点![]() 的整个运动过程中,
的整个运动过程中,
①直接用含![]() 的代数式表示点
的代数式表示点![]() 的坐标.
的坐标.
②利用(2)的结论,以![]() 为直角顶点作等腰直角
为直角顶点作等腰直角![]() (点
(点![]() 按逆时针顺序排列).当
按逆时针顺序排列).当![]() 与
与![]() 的一边平行时,求所有满足条件的
的一边平行时,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(bigdata)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是根据调查结果绘制出不完整的两个统计图表:
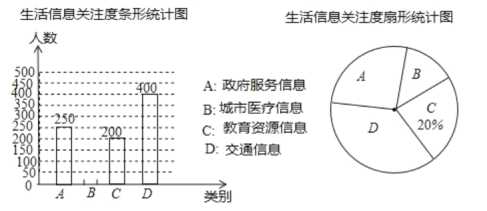
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是________,扇形统计图中![]() 部分的圆心角的度数是________,并补全条形统计图;
部分的圆心角的度数是________,并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是________类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程ax2+2x﹣3=0有两个不相等的实数根.
(1)求a的取值范围;
(2)若此方程的一个实数根为1,求a的值及方程的另一个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
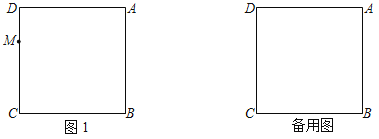
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
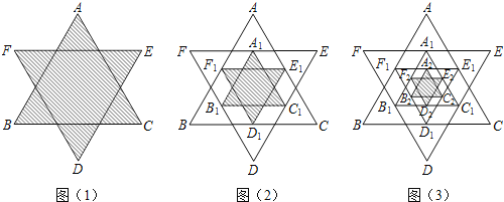
【题目】如图(1) ,将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和1D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E 2F 2,如图(3) 中阴影部分;如此下去…,则正六角星形AnFnBnDnCnE nF n的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
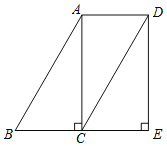
【题目】如图,在ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com