
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD. 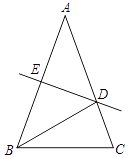
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
【答案】
(1)解:∵∠ABC=∠C,∠A=40°,
∴∠ABC=(180°﹣40°)÷2=70°.
∵DE是边AB的垂直平分线,
∴AD=DB,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°
(2)解:∵DE是边AB的垂直平分线,
∴AD=DB,AE=BE,
∵△BCD的周长为18cm,
∴AC+BC=AD+DC+BC=DB+DC+BC=18cm.
∵△ABC的周长为30cm,
∴AB=30﹣(AC+BC)=30﹣18=12cm,
∴BE=12÷2=6cm
【解析】(1)首先计算出∠ABC的度数,再根据线段垂直平分线上任意一点,到线段两端点的距离相等可得AD=BD,进而可得∠ABD=∠A=40°,然后可得答案;(2)根据线段垂直平分线的性质可得AD=DB,AE=BE,然后再计算出AC+BC的长,再利用△ABC的周长为30cm可得AB长,进而可得答案.
【考点精析】关于本题考查的三角形的内角和外角和线段垂直平分线的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF. 
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可以到甲乙两个商店购买,已知商店的标价都是每本2元,甲店的优惠条件是:购买10本以上,从第11本开始按标价的70%出售,乙商店的优惠条件是:从第一本起按标价的80%出售. ①若小明要购买x本练习本,则小明到甲店购买,需付款元,当到乙店购买时,需付款元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙、丙三位同学分别设计出如下几种方案: 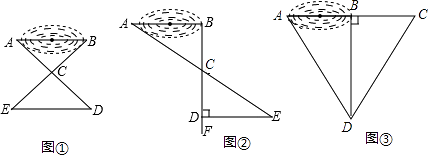
甲:如图①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的长即为A,B的距离.
乙:如图②,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离.
丙:如图③,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A,B的距离.
(1)以上三位同学所设计的方案,可行的有;
(2)请你选择一可行的方案,说说它可行的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)如图①,BF垂直CE于点F,交CD于点G,试说明AE=CG; 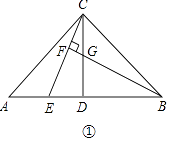
(2)如图②,作AH垂直于CE的延长线,垂足为H,交CD的延长线于点M,则图中与BE相等的线段是 , 并说明理由. 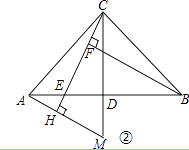
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com