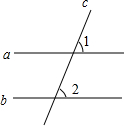如图.已知直线a∥b.∠1=70°.则∠2=70度．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

13．

如图，已知直线a∥b，∠1=70°，则∠2=70度．

分析由两直线平行，同位角相等，即可得出结果．

解答解：∵a∥b，
∴∠2=∠1=70°（两直线平行，同位角相等）．
故答案为：70．

点评本题考查了平行线的性质：两直线平行，同位角相等；熟练掌握平行线的性质，并能进行推理论证是解决问题的关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

3．

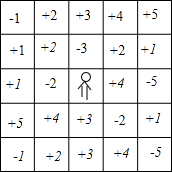如图是一个“冲出围城”的游戏，规则是：城中人想要冲出围城，可以横走也可以竖走，但不可以斜走，每走一格就可以得到格中相应的分数作为生命值，每格中的分数用乘法累计．当生命值小于+9，并且处于最外圈时，就可以冲出围城，生命值为负数不可以出城．例如：（-2）×（+2）×（+2）×（-1）=+8，就是一条冲出围城的路线．把你找到的冲出围城的路线写下来，也可以直接用箭头将路线在表中表示出来．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．解方程组或不等式组：
（1）$\left\{\begin{array}{l}{3x=2y}\\{x-4y=5}\end{array}\right.$
（2）$\left\{\begin{array}{l}{5x+2＜3（x+2）}\\{\frac{x-1}{2}≤\frac{2x-1}{3}}\end{array}\right.$
（3）解不等式组$\left\{\begin{array}{l}{x+1＞0}\\{2（x+1）≥3x-1}\end{array}\right.$，并求其整数解．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．如图，在矩形ABCD中，AB=$\sqrt{3}$，BC=3，在BC边上有2个点E、F（E在F的左边），以EF为边长作等边三角形PEF，使点P恰好落在边AD上，PF交AC于点H．
（1）求△PEF的边长；
（2）如图1，当CF＜1的时候，试猜想PH与BE的数量关系，并证明你的结论；
（3）如图2，当CF＞2的时候，其他条件不变（2）中的结论还成立吗？如果成立，请说明理由；如果不成立，请直接写出结论．