
 在六边形ABCDEF中,AF∥CD,∠A=∠D,∠B=∠E,那么BC∥EF吗?为什么?
在六边形ABCDEF中,AF∥CD,∠A=∠D,∠B=∠E,那么BC∥EF吗?为什么? 分析 延长BA和EF交于N,延长CD和FE交于O,延长AB和DC交于M,根据平行线的性质得出∠FAB+∠M=180°,求出∠EDO=∠M,根据平行线的判定得出DE∥AB,根据平行线的性质得出∠N+∠FED=180°,求出∠N=∠MBC,根据平行线的判定得出即可.
解答 解:BC∥EF,理由是:
如图,延长BA和EF交于N,延长CD和FE交于O,延长AB和DC交于M,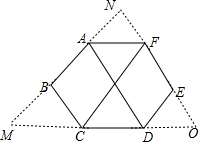
∵AF∥CD,
∴∠FAB+∠M=180°,
∵∠EDO+∠CDE=180°,∠CDE=∠FAB,
∴∠EDO=∠M,
∴DE∥AB,
∴∠N+∠FED=180°,
∵∠ABC=∠FED,∠MBC+∠ABC=180°,
∴∠N=∠MBC,
∴BC∥EF.
点评 本题考查了平行线的性质和判定的应用,能综合运用平行线的性质和判定定理进行推理是解此题的关键,难度适中.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,某位同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时的刻度为12cm,已知手臂长为60cm,求电线杆的高度.
如图,某位同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时的刻度为12cm,已知手臂长为60cm,求电线杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1解析式为y=2x+4与x轴交于点A,直线l2是由直线y=-x-1向上平移2个单位得到的,其中与x轴交于点B,与l1交于点C.已知A(-2,0),直线l2解析式为y=-x+1,△ABC的面积为3,在直线l2上存在异于点C的另一点P,使得△APB与△ABC的面积相等,求出点P的坐标.
如图,直线l1解析式为y=2x+4与x轴交于点A,直线l2是由直线y=-x-1向上平移2个单位得到的,其中与x轴交于点B,与l1交于点C.已知A(-2,0),直线l2解析式为y=-x+1,△ABC的面积为3,在直线l2上存在异于点C的另一点P,使得△APB与△ABC的面积相等,求出点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.
如图,AC⊥BC,AC=BC=2,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作⊙C,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是$\frac{5}{12}$π-$\frac{1}{2}$$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知如图,矩形OCBD如图所示,OD=2,OC=3,反比例函数的图象经过点B,点A为第一象限双曲线上的动点(点B除外),过点A作AF⊥BD于点F,AE⊥x轴于点E,若矩形OCBD和矩形AEDF相似,则点A的坐标是($\sqrt{5}$+1,$\frac{3\sqrt{5}-3}{2}$)或($\sqrt{10}$+1,$\frac{2\sqrt{10}-2}{3}$).
已知如图,矩形OCBD如图所示,OD=2,OC=3,反比例函数的图象经过点B,点A为第一象限双曲线上的动点(点B除外),过点A作AF⊥BD于点F,AE⊥x轴于点E,若矩形OCBD和矩形AEDF相似,则点A的坐标是($\sqrt{5}$+1,$\frac{3\sqrt{5}-3}{2}$)或($\sqrt{10}$+1,$\frac{2\sqrt{10}-2}{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com