
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊОиаЮЃЌABЃН4cmЃЌADЃН3cmЃЌЖЏЕуMЃЌNЗжБ№ДгЕуDЃЌBЭЌЪБГіЗЂЃЌЖМвд1cm/sЕФЫйЖШдЫЖЏЃЎЕуMбиDAЯђжеЕуAдЫЖЏЃЌЕуNбиBCЯђжеЕуCдЫЖЏЃЎЙ§ЕуNзїNPЁЭBCЃЌНЛACгкЕуOЃЌСЌНгMPЃЎвбжЊЖЏЕудЫЖЏСЫtsЃЈ0ЃМtЃМ3ЃЉЃЎ
ЃЈ1ЃЉЕБtЮЊЖрЩйЪБЃЌPMЁЮABЃП
ЃЈ2ЃЉШєЫФБпаЮCDMPЕФУцЛ§ЮЊSЃЌЪдЧѓSгыtЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬtЪЙЫФБпаЮCDMPУцЛ§гыЫФБпаЮABCDУцЛ§БШЮЊ3ЃК8ЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉдкЕуMЃЌNдЫЖЏЙ§ГЬжаЃЌЁїMPAФмЗёГЩЮЊвЛИіЕШбќШ§НЧаЮЃПШєФмЃЌЧѓГіЫљгаПЩФмЕФtжЕЃЛШєВЛФмЃЌЪдЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉЕБt=![]() ЪБЃЌPMЁЮABЃЛЃЈ2ЃЉsЃН
ЪБЃЌPMЁЮABЃЛЃЈ2ЃЉsЃН![]() t2Љ2t+6ЃЛЃЈ3ЃЉtЃН
t2Љ2t+6ЃЛЃЈ3ЃЉtЃН![]() ЪБЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЛЃЈ4ЃЉЕБtЃН1ЛђtЃН
ЪБЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЛЃЈ4ЃЉЕБtЃН1ЛђtЃН![]() ЛђtЃН
ЛђtЃН![]() ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЬѕМўЕУЕНPMгыPNЙВжБЯпЃЌЧѓЕУMNЁЮABЃЌСаЗНГЬМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉбгГЄNPНЛADгкЕуQЃЌдђPQЁЭADЃЌгЩЁїPNCЁзЁїABCЕУ![]() МД
МД![]() ИљОнSЫФБпаЮCDMPЃНSЁїACDЉSЁїAMPПЩЕУЃЛ
ИљОнSЫФБпаЮCDMPЃНSЁїACDЉSЁїAMPПЩЕУЃЛ
ЃЈ3ЃЉгЩ![]() НтЗНГЬПЩЕУЃЛ
НтЗНГЬПЩЕУЃЛ
ЃЈ4ЃЉБОЬтвЊЗжШ§жжЧщПіЃКЂйMPЃНPAЃЌФЧУДAQЃНBNЃН![]() AMЃЌПЩгУxЗжБ№БэЪОГіBNКЭAMЕФГЄЃЌШЛКѓИљОнЩЯЪіЕШСПЙиЯЕПЩЧѓЕУxЕФжЕЃЎЂкMAЃНMPЃЌдкжБНЧШ§НЧаЮMQPжаЃЌMQЃНMAЉBNЃЌPQЃНABЉPNИљОнЙДЙЩЖЈРэМДПЩЧѓГіxЕФжЕЃЎЂлMAЃНPAЃЌВЛФбЕУГіAPЃН
AMЃЌПЩгУxЗжБ№БэЪОГіBNКЭAMЕФГЄЃЌШЛКѓИљОнЩЯЪіЕШСПЙиЯЕПЩЧѓЕУxЕФжЕЃЎЂкMAЃНMPЃЌдкжБНЧШ§НЧаЮMQPжаЃЌMQЃНMAЉBNЃЌPQЃНABЉPNИљОнЙДЙЩЖЈРэМДПЩЧѓГіxЕФжЕЃЎЂлMAЃНPAЃЌВЛФбЕУГіAPЃН![]() BNЃЌШЛКѓгУxБэЪОГіAMЕФГЄЃЌМДПЩЧѓГіxЕФжЕЃЎ
BNЃЌШЛКѓгУxБэЪОГіAMЕФГЄЃЌМДПЩЧѓГіxЕФжЕЃЎ
НтЃКЃЈ1ЃЉЁпPMЁЮABЃЌABЁЮPNЃЌ
ЁрPMгыPNЙВжБЯпЃЌ
ЁрMNЁЮABЃЌ
ЁрAMЃНNBЃЌ
Ёр3ЉtЃНtЃЌ
ЕУ![]()
ЃЈ2ЃЉШчЭМЃЌбгГЄNPНЛADгкЕуQЃЌдђPQЁЭADЃЌ

гЩЬтвтжЊЃЌDMЃНBNЃНtЃЌAMЃНCNЃН3ЉtЃЌ
ЁпPNЁЮABЃЌ
ЁрЁїPNCЁзЁїABCЃЌ
Ёр![]() МД
МД![]()
НтЕУЃК ![]()
ЁпPQЁЭADЃЌ
ЁрЁЯQABЃНЁЯBЃНЁЯNQAЃН90ЁуЃЌ
ЁрЫФБпаЮABNQЪЧОиаЮЃЌ
дђABЃНQNЃН4ЃЌ
Ёр![]()
ЁрЫФБпаЮCDMPЕФУцЛ§![]()
ЃЈ3ЃЉЁпSОиаЮABCDЃН3ЁС4ЃН12ЃЌ
Ёр![]()
НтЕУЃК![]()
Ыљвд![]() ЪБЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЛ
ЪБЫФБпаЮCDMPЕФУцЛ§гыЫФБпаЮABCDЕФУцЛ§БШЮЊ3ЃК8ЃЛ
ЃЈ4ЃЉЁїMPAФмГЩЮЊЕШбќШ§НЧаЮЃЌЙВгаШ§жжЧщПіЃЌвдЯТЗжРрЫЕУїЃК
ЂйШєPMЃНPAЃЌ
ЁпPQЁЭMAЃЌ
ЁрЫФБпаЮABNQЪЧОиаЮЃЌ
ЁрQAЃНNBЃНtЃЌ
ЁрMQЃНQAЃНtЃЌ
гжЁпDM+MQ+QAЃНAD
Ёр3tЃН3ЃЌМДtЃН1
ЂкШєMPЃНMAЃЌдђMQЃН3Љ2tЃЌ![]() MPЃНMAЃН3ЉtЃЌ
MPЃНMAЃН3ЉtЃЌ
дкRtЁїPMQжаЃЌгЩЙДЙЩЖЈРэЕУЃКMP2ЃНMQ2+PQ2
Ёр![]()
НтЕУЃКtЃН![]() ЃЈtЃН0ВЛКЯЬтвтЃЌЩсШЅЃЉ
ЃЈtЃН0ВЛКЯЬтвтЃЌЩсШЅЃЉ
ЂлШєAPЃНAMЃЌ
гЩЬтвтПЩЕУЃКAPЃН![]() tЃЌAMЃН3Љt
tЃЌAMЃН3Љt
Ёр![]()
НтЕУЃКtЃН![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕБtЃН1ЛђtЃН![]() ЛђtЃН
ЛђtЃН![]() ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїMPAЪЧЕШбќШ§НЧаЮЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпГЄЮЊ4cmЃЌЁЯAЃН60ЁуЃЌЛЁBDЪЧвдЕуAЮЊдВаФЃЌABГЄЮЊАыОЖЕФЛЁЃЌЛЁCDЪЧвдЕуBЮЊдВаФЃЌBCГЄЮЊАыОЖЕФЛЁЃЌдђвѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ

A. 2cm2B. 4![]() cm2C. 4cm2D. Іаcm2
cm2C. 4cm2D. Іаcm2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃдквЛДЮДѓПЮМфЛюЖЏжаЃЌВЩгУСЫЫФжгЛюЖЏаЮЪНЃКAЁЂХмВНЃЌBЁЂЬјЩўЃЌCЁЂзіВйЃЌDЁЂгЮЯЗ.ШЋаЃбЇЩњЖМбЁдёСЫвЛжжаЮЪНВЮгыЛюЖЏЃЌаЁНмЖдЭЌбЇУЧбЁгУЕФЛюЖЏаЮЪННјааСЫЫцЛњГщбљЕїВщЃЌИљОнЕїВщЭГМЦНсЙћЃЌЛцжЦСЫВЛЭъећЕФЭГМЦЭМ.


ЧыНсКЯЭГМЦЭМЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщбЇЩњЙВ ШЫЃЌ ![]() = ЃЌВЂНЋЬѕаЮЭМВЙГфЭъећЃЛ
= ЃЌВЂНЋЬѕаЮЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉШчЙћИУаЃгабЇЩњ2000ШЫЃЌЧыФуЙРМЦИУаЃбЁдёЁАХмВНЁБетжжЛюЖЏЕФбЇЩњдМгаЖрЩйШЫЃП
ЃЈ3ЃЉбЇаЃШУУПАрдкAЁЂBЁЂCЁЂDЫФжгЛюЖЏаЮЪНжаЃЌЫцЛњГщШЁСНжжПЊеЙЛюЖЏЃЌЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓУПАрГщШЁЕФСНжжаЮЪНЧЁКУЪЧЁАХмВНЁБКЭЁАЬјЩўЁБЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§АыОЖЮЊ2ЕФЁбOЭтвЛЕуPЃЌзїЁбOЕФЧаЯпPAЃЌЧаЕуЮЊAЃЌСЌНгPOЃЌНЛЁбOгкЕуCЃЌЙ§ЕуAзїЁбOЕФЯвABЃЌЪЙABЁЮPOЃЌСЌНгPBЁЂBCЃЎ
ЃЈ1ЃЉЕБЕуCЪЧPOЕФжаЕуЪБЃЌ
ЂйЧѓжЄЃКЫФБпаЮPABCЪЧЦНааЫФБпаЮЃЛ
ЂкЧѓЁїPABЕФУцЛ§ЃЎ
ЃЈ2ЃЉЕБABЃН2![]() ЪБЃЌЧыжБНгаДГіPCЕФГЄЖШЃЎ
ЪБЃЌЧыжБНгаДГіPCЕФГЄЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙВЯэЕЅГЕЮЊШЫУЧЕФЩњЛюДјРДСЫМЋДѓЕФБуРћЃЎШчЭМЃЌвЛСОЕЅГЕЗХдкЫЎЦНЕФЕиУцЩЯЃЌГЕАбЭЗЯТЗНAДІгызјЕцЯТЗНBДІдкЦНаагкЕиУцЕФЫЎЦНЯпЩЯЃЌAЃЌBжЎМфЕФОрРыЮЊ49cmЃЌЯжВтЕУACЃЌBCгыABЕФМаНЧЗжБ№ЮЊ45ЁуЃЌ68ЁуЃЎШєЕуCЕНЕиУцЕФОрРыCDЮЊ28cmЃЌзјЕцжажсEДІгыЕуBЕФОрРыBEЮЊ5cmЃЌЧѓЕуEЕНЕиУцЕФОрРыЃЎЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЌВЮПМЪ§ОнЃКsin68ЁуЁж0.93ЃЌcos68ЁуЁж0.37ЃЌtan68ЁуЁж2.50ЃЎЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЕФЪЧЮчанЪБРЯЪІУЧЫљгУЕФвЛжжелЕўвЮЃЌЯжНЋЬЩвЮвдШчЭМ2ЫљЪОЕФЗНЪНЧуаБЗХжУЃЌAMгыЕиУцMEГЩ45ЁуНЧЃЌABЁЮMEЃЌвЮБГBCгыЫЎЦНЯпГЩ30ЁуНЧЃЌЦфжаAMЃН50РхУзЃЌBCЃН72РхУзЃЌBPЪЧЬЩвЮЕФЩьЫѕжЇМмЃЌЧв30ЁуЁмBPMЁм90ЁуЃЎ(НсЙћОЋШЗЕН1РхУзЃЛВЮПМЪ§Он![]() Ёж1.4ЃЌ
Ёж1.4ЃЌ![]() Ёж 1.7ЃЌ
Ёж 1.7ЃЌ![]() Ёж 2.2)
Ёж 2.2)

(1)ЧѓДЫЪБЕуCгыЕиУцЕФОрРыЃЎ
(2)дк(1)ЕФЬѕМўЯТЃЌЧѓЩьЫѕжЇМмBPПЩДяЕНЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
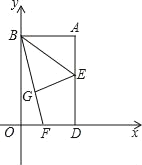
ЁОЬтФПЁПШчЭМЃЌвдОиаЮABODЕФСНБпODЁЂOBЮЊзјБъжсНЈСЂжБНЧзјБъЯЕЃЌШєEЪЧADЕФжаЕуЃЌНЋЁїABEбиBEелЕўКѓЕУЕНЁїGBEЃЌбгГЄBGНЛODгкFЕуЃЎШєOFЃНIЃЌFDЃН2ЃЌдђGЕуЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпx=1ЃЌгыyжсЕФНЛЕуBдкЃЈ0ЃЌ2ЃЉКЭЃЈ0ЃЌ3ЃЉжЎМфЃЈАќРЈетСНЕуЃЉЃЌЯТСаНсТлЃК
ЂйЕБxЃО3ЪБЃЌyЃМ0ЃЛЂк3a+bЃМ0ЃЛЂлЉ1ЁмaЁмЉ![]() ЃЛЂм4acЉb2ЃО8aЃЛ
ЃЛЂм4acЉb2ЃО8aЃЛ
Цфжае§ШЗЕФНсТлЪЧЃЈ ЃЉ

AЃЎЂйЂлЂм BЃЎЂйЂкЂл CЃЎЂйЂкЂм DЃЎЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
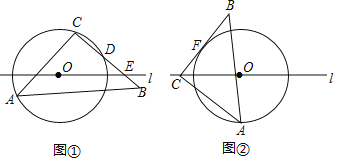
ЁОЬтФПЁПвбжЊЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BC=8ЃЌЕуAдкАыОЖЮЊ5ЕФЁбOЩЯЃЌЕуOдкжБЯпlЩЯЃЎ
(1)ШчЭМЂйЃЌШєЁбOОЙ§ЕуCЃЌНЛBCгкЕуDЃЌЧѓCDЕФГЄЃЎ
(2)дк(1)ЕФЬѕМўЯТЃЌШєBCБпНЛlгкЕуEЃЌOE=2![]() ЃЌЧѓBEЕФГЄЃЎ
ЃЌЧѓBEЕФГЄЃЎ
(3)ШчЭМЂкЃЌШєжБЯпlЛЙОЙ§ЕуCЃЌBCЪЧЁбO ЕФЧаЯпЃЌFЮЊЧаЕуЃЌдђCFЕФГЄЮЊ____ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com