
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
【答案】(1)![]() (2)不存在
(2)不存在
【解析】
(1)由题意可得△≥0,即[﹣(2k+1)]2﹣4(k2+2k)≥0,通过解该不等式即可求得k的取值范围;
(2)假设存在实数k使得x1·x2-x12-x22≥0成立.由根与系数的关系可得x1+x2=2k+1,x1·x2=k2+2k,然后利用完全平方公式可以把x1·x2-x12-x22≥0转化为3x1·x2-(x1+x2)2≥0的形式,通过解不等式可以求得k的值.
(1)∵原方程有两个实数根,
∴△≥0
即[﹣(2k+1)]2﹣4(k2+2k)≥0,
∴4k2+4k+1﹣4k2﹣8k≥0 ,
∴1﹣4k≥0,
∴k≤![]() ,
,
∴当k≤![]() 时,原方程有两个实数根;
时,原方程有两个实数根;
(2)假设存在实数k使得x1·x2-x12-x22≥0成立,
∵x1,x2是原方程的两根,
∴x1+x2=2k+1,x1·x2=k2+2k,
由x1·x2-x12-x22≥0,
得3x1·x2-(x1+x2)2≥0
∴3(k2+2k)﹣(2k+1)2≥0,
整理得:﹣(k﹣1)2≥0,
∴只有当k=1时,上式才能成立;
又∵由(1)知k≤![]() ,
,
∴不存在实数k使得x1·x2-x12-x22≥0成立.


科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)~(3)题.
数学课上,老师出示了这样一道题:
如图1,△ABC中,AC=BC=a,∠ACB=90°,点D在AB上,且AD=kAB(其中0<k<![]() ),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现DC与DE相等”;
小伟:“通过构造全等三角形,经过进一步推理,可以得到DC与DE相等”
小强:“通过进一步的推理计算,可以得到BE与BC的数量关系”
老师:“保留原题条件,连接CE交AB于点O.如果给出BO与DO的数量关系,那么可以求出COEO的值”
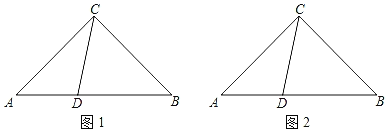
(1)在图1中将图补充完整,并证明DC=DE;
(2)直接写出线段BE与BC的数量关系 (用含k的代数式表示);
(3)在图2中将图补充完整,若BO=![]() DO,求COEO的值(用含a的代数式表示).
DO,求COEO的值(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:3,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为( )
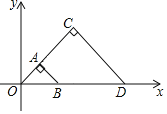
A.(3,3)B.(2,4)C.(![]() ,2
,2![]() )D.(4,4)
)D.(4,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假快到了,父母找算带兄妹俩去某个景点旅游一次,长长见识,可哥哥坚持去黄山,妹妹坚持去泰山,争执不下,父母为了公平起见,决定设计一款游戏,若哥哥赢了就去黄山,妹妹赢了就去泰山.下列游戏中,不能选用的是( )
A. 掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢
B. 同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢
C. 掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢
D. 在不透明的袋子中装有两黑两红四个球,除颜色外,其余均相同,随机摸出一个是黑球则哥哥赢,是红球则妹妹赢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.

(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
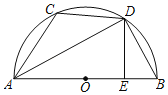
【题目】如图,四边形ABDC内接于半圆O,AB为直径,AD平分∠CAB,AB﹣AC=4,AD=3![]() ,作DE⊥AB于点E,则BE的长为_____,AC的长为_____.
,作DE⊥AB于点E,则BE的长为_____,AC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
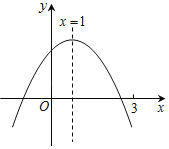
A.①②③B.②④C.②⑤D.②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com