
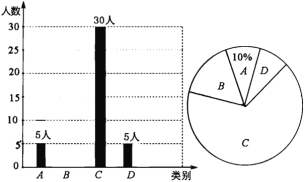
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
【答案】(1)50,216°;(2)补图见解析;(3)180;(4)![]()
【解析】(1)由A类别人数及其所占百分比可得总人数,用360°乘以C部分人数所占比例可得;
(2)总人数减去其他类别人数求得B的人数,据此即可补全条形图;
(3)用总人数乘以样本中A类别人数所占百分比可得;
(4)用树状图或列表法即可求出抽到性别相同的两个学生的概率.
(1)被调查的总人数为5÷10%=50人,扇形统计图中C部分所对应的扇形圆心角的度数为360°×![]() =216°,
=216°,
(2)B类别人数为50-(5+30+5)=10人,
补全图形如下:
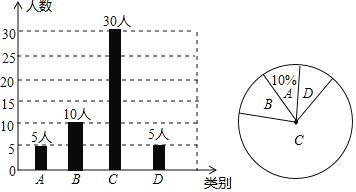
(3)估计该校学生中A类有1800×10%=180人;
(4)列表如下:
女1 | 女2 | 女3 | 男1 | 男2 | |
女1 | --- | 女2女1 | 女3女1 | 男1女1 | 男2女1 |
女2 | 女1女2 | --- | 女3女2 | 男1女2 | 男2女2 |
女3 | 女1女3 | 女2女3 | --- | 男1女3 | 男2女3 |
男1 | 女1男1 | 女2男1 | 女3男1 | --- | 男2男1 |
男2 | 女1男2 | 女2男2 | 女3男2 | 男1男2 | --- |
所有等可能的结果为20种,其中被抽到的两个学生性别相同的结果数为8,
∴被抽到的两个学生性别相同的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐场为了有稳定的客源,决定开办会员业务,每张会员证30元,只限本人使用,有效期为一年,凭证入场每人次收费2元,不凭证入场每人次收费3元.
(1)一年内在这个游乐场玩多少次,办理会员证和不办理会员证花钱一样多?
(2)2019年,小明计划每月到游乐场玩4次,请你为他推荐一种经济省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.

(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.
(1)请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
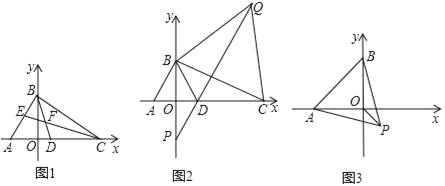
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,已知点A(m,0),B(n,0),且m,n满足(m+1)2+![]() =0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
=0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
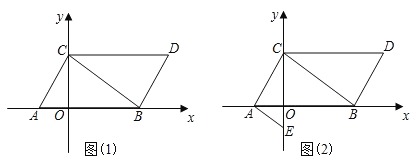
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形PBC的面积等于平行四边形ABDC的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且∠BAE=∠DCB.求证:AE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
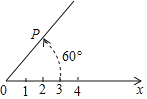
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3(__________________________)
又∵HG∥CD(已知)
∴∠2=∠4(_______________________________)
∵AB∥CD(已知)
∴∠BEF+___________=180°(_____________________)
又∵EG平分∠BEF,FG平分∠EFD (已知)
∴∠1=(______)∠BEF,∠2=(______)∠EFD (______________________)
∴∠1+∠2=(________) (∠BEF +∠EFD)=(____________)
∴∠3+∠4=90°(_______________________)即∠EGF=90°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com