

���� ��1����ͼ�٣���CDƽ�֡�ABC������ɵ�AD=DB��ֻ�����AB�Ϳɽ�����⣻
��2����ͼ�ڣ���AEƽ�֡�ABC������ɵ�CE=EB=2���ɴ˿ɵ�AC+CE��AB+EB����AE���ǡ��ȷֻ����ߡ���
��3����ͼ�ۣ���MN�ǡ��ȷֻ����ߡ��ɵ�CM+CN=6��S��MCN=$\frac{1}{2}$CM•CN=3���Ӷ��ɵ�$\frac{1}{2}$x��6-x��=3�����x���ɵ�M��BC�ϣ���N��AC�Ͽɵ�3��x��4���Ӷ��ɵá��ȷֻ����ߡ������ڣ�
��4����ͼ�ܣ���PQ�ǡ��ȷֻ����ߡ��ɵ�AP+AQ=6��S��APQ=$\frac{1}{2}$S��ABC=3����AP=x����AQ=6-x������P��PH��AQ��H����֤��AHP�ס�ACB���������������ε����ʿɵ�PH=$\frac{4x}{5}$����S��APQ=3�����x���ɵ�P��AC�ϣ���Q��AB�Ͽɵ�1��x��3���Ӷ��ɵõ�x��ֵ�����ɵõ�AP��AQ��ֵ��
��� �⣺��1����ͼ�٣�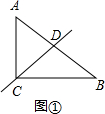
�ߡ�ACB=90�㣬AC=3��BC=4��
��AB=5��
��CDƽ�֡�ABC�������
��AD=DB��
��AD=$\frac{1}{2}$AB=$\frac{5}{2}$��
�ʴ�Ϊ$\frac{5}{2}$��
��2��AE���ǡ��ȷֻ����ߡ���
���ɣ���ͼ�ڣ�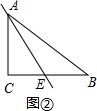
��AEƽ�֡�ABC�������
��CE=EB=$\frac{1}{2}$BC=2��
��AC+CE=3+2=5��AB+EB=5+2=7��
��AC+CE��AB+EB��
��AE���ǡ��ȷֻ����ߡ���
��3����ͼ�ۣ�
��ֱ��MNƽ�֡�ABC���ܳ���
��CM+CN=$\frac{1}{2}$��3+4+5��=6��
��MC=x����CN=6-x��
��ֱ��MNƽ�֡�ABC�������
��S��MCN=$\frac{1}{2}$S��ABC=$\frac{1}{2}$��$\frac{1}{2}$��4��3=3��
��$\frac{1}{2}$CM•CN=3��
��$\frac{1}{2}$x��6-x��=3��
������x2-6x+6=0��
���x1=3+$\sqrt{3}$��x2=3-$\sqrt{3}$��
�ߵ�M��BC�ϣ���N��AC�ϣ�
��x��4��6-x��3��
��3��x��4��
��x�����ڣ�
�ࡰ�ȷֻ����ߡ������ڣ�
��4����ͼ�ܣ�PQ�ǡ��ȷֻ����ߡ���
����AP+AQ=6��S��APQ=$\frac{1}{2}$S��ABC=3��
��AP=x����AQ=6-x��
����P��PH��AQ��H��
���С�AHP=��C=90�㣮
�ߡ�A=��A��
���AHP�ס�ACB��
��$\frac{PH}{BC}$=$\frac{AP}{AB}$��
��$\frac{PH}{4}$=$\frac{x}{5}$��
��PH=$\frac{4x}{5}$��
��S��APQ=$\frac{1}{2}$AQ•PH=$\frac{1}{2}$��6-x��•$\frac{4x}{5}$=3��
������2x2-12x+15=0��
���x1=$\frac{6+\sqrt{6}}{2}$��x2=$\frac{6-\sqrt{6}}{2}$��
�ߵ�P��AC�ϣ���Q��AB�ϣ�
��x��3��6-x��5��
��1��x��3��
��x=$\frac{6-\sqrt{6}}{2}$��
��6-x=$\frac{6+\sqrt{6}}{2}$��
��AP=$\frac{6-\sqrt{6}}{2}$��AQ=$\frac{6+\sqrt{6}}{2}$��
���P�����A$\frac{6-\sqrt{6}}{2}$������Q�����A$\frac{6+\sqrt{6}}{2}$����
���� ������Ҫ���������������ε��ж������ʣ���һԪ���η��̡����ɶ����������ε�����ƽ�������ε������֪ʶ����Ҫ˵�����ǣ�����ڣ�3��С�⼰�ڣ�4��С��Ĺ����У�Ҫ����x��ȡֵ��Χ�����⣬�ڣ�4��С�����Ĺ�����û�п���ֱ�����BC��AB�ཻ�����������Ϊͨ�������֪������¡��ȷֻ����ߡ������ڣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a��50-a��}{2}cm$2 | B�� | $\frac{a��50-2a��}{4}cm$2 | C�� | a��50-2a��cm2 | D�� | a��25-a��cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x2+x | B�� | 2x2-3x | C�� | x+$\frac{1}{2}$ | D�� | x-$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com