
分析 设A(m,0),B(n,0),由△AOC∽△COB,得$\frac{OA}{CO}$=$\frac{CO}{OB}$结合根与系数关系,列出方程即可解决问题
解答 解:∵抛物线y=ax2+2x-5与x轴交于A、B两点,交y轴于点C,
∴C(0,-5),设A(m,0),B(n,0),如图所示,
∵∠ACB=90°,
∴∠CAO+∠ABC=90°,∠ABC+∠OCB=90°,
∴∠OAC=∠OCB,∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴$\frac{OA}{CO}$=$\frac{CO}{OB}$,
∴$\frac{-m}{5}$=$\frac{5}{n}$,
∴mn=-25=-$\frac{5}{a}$,
∴a=$\frac{1}{5}$,
故答案为$\frac{1}{5}$.
点评 本题考查抛物线与x轴的交点、相似三角形的判定和性质、根与系数关系等知识,解题的关键是灵活应用这些知识解决问题,学会利用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | x0,y0均为偶数 | B. | x0,y0均为奇数 | ||
| C. | x0是偶数,y0是奇数 | D. | x0是奇数,y0是偶数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
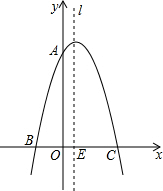 已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.
已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )
如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com