
 如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )
如图,在△ABC中,AB=AC,tan∠B=2,BC=3$\sqrt{2}$.边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°.设BE=x,MN=y,则能表示y与x的函数关系的大致图象是( )| A. | 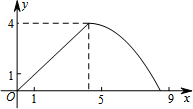 | B. |  | ||
| C. |  | D. | 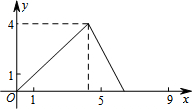 |
分析 分两种情况讨论:①当点N在边BC时,点E与N重合如图1,此时0<x≤3$\sqrt{2}$.过点M作MG⊥BC于点G,解等腰直角三角形MGN,得出GN=$\frac{\sqrt{2}}{2}$y.由tan∠B=2,得出BG=$\frac{\sqrt{2}}{4}$y.由BG+GE=BE得到$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{4}$y=x,即y=$\frac{2\sqrt{2}}{3}$x;②当点N在BC延长线上时,如图2,此时3$\sqrt{2}$<x≤$\frac{9\sqrt{2}}{2}$.过点M作MG⊥BC于点G,过点N作NF⊥BC于点F,过点N作NH⊥MG于点H,设NE=a,求出MH=HN=GF=$\frac{\sqrt{2}}{2}$y,NF=FE=$\frac{\sqrt{2}}{2}$a,MG=GE=$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{2}$a=$\frac{\sqrt{2}}{2}$(y+a),BG=$\frac{\sqrt{2}}{4}$(y+a).由BC=BG+GF+FC,得出$\frac{\sqrt{2}}{4}$(y+a)+$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{4}$a=3$\sqrt{2}$,即a=$\frac{12-3y}{2}$.再根据BG+GF+FE=BE得到$\frac{\sqrt{2}}{8}$(12-y)+$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{4}$(12-3y)=x,即y=-$\frac{4\sqrt{2}}{3}$x+12.
解答  解:分两种情况:
解:分两种情况:
①当点N在边BC时,点E与N重合,如图1,此时0<x≤3$\sqrt{2}$.
过点M作MG⊥BC于点G,
∵∠MNG=45°,∴MG=GN=$\frac{\sqrt{2}}{2}$y.
∵tan∠B=2,∴BG=$\frac{\sqrt{2}}{4}$y.
∵BG+GE=BE,
∴$\frac{\sqrt{2}}{4}$y+$\frac{\sqrt{2}}{2}$y=x,即y=$\frac{2\sqrt{2}}{3}$x;
②当点N在BC延长线上时,如图2,此时3$\sqrt{2}$<x≤$\frac{9\sqrt{2}}{2}$.
过点M作MG⊥BC于点G,过点N作NF⊥BC于点F,过点N作NH⊥MG于点H,设NE=a,
∵∠MEG=45°,HN∥BC,
∴MH=HN=$\frac{\sqrt{2}}{2}$y,NF=FE=$\frac{\sqrt{2}}{2}$a,MG=GE=$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{2}$a=$\frac{\sqrt{2}}{2}$(y+a).
∵AB=AC,tan∠B=2,∴tan∠NCF=2.∴FC=$\frac{\sqrt{2}}{4}$a.
又∵tan∠B=2,∴BG=$\frac{\sqrt{2}}{4}$(y+a).
∵BC=BG+GF+FC,GF=HN,∴$\frac{\sqrt{2}}{4}$(y+a)+$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{4}$a=3$\sqrt{2}$,
∴a=$\frac{12-3y}{2}$.
∴FE=$\frac{\sqrt{2}}{2}$a=$\frac{\sqrt{2}}{4}$(12-3y),BG=$\frac{\sqrt{2}}{4}$(y+$\frac{12-3y}{2}$)=$\frac{\sqrt{2}}{8}$(12-y),
∴$\frac{\sqrt{2}}{8}$(12-y)+$\frac{\sqrt{2}}{2}$y+$\frac{\sqrt{2}}{4}$(12-3y)=x,即y=-$\frac{4\sqrt{2}}{3}$x+12.
综上所述,y与x的函数关系为y=$\left\{\begin{array}{l}{\frac{2\sqrt{2}}{3}x(0<x≤3\sqrt{2})}\\{-\frac{4\sqrt{2}}{3}x+12(3\sqrt{2}<x≤\frac{9\sqrt{2}}{2})}\end{array}\right.$.
故选D.
点评 本题考查了动点问题的函数图象,等腰三角形的性质,等腰直角三角形的判定和性质,锐角三角函数的定义,利用数形结合与分类讨论是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 36,8 | B. | 28,6 | C. | 28,8 | D. | 13,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.
如图,AB是⊙O的直径,点C在⊙O上,D是⊙O上的一个动点,且C,D两点位于直径AB的两侧.连接CD,过点C作CE⊥CD交DB的延长线于点E.若AC=2,BC=4,则线段DE长的最大值是10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
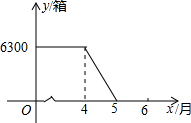 某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.
某工厂生产空气清新剂,今年4月份后,每天的产量与销售量均为500箱,进入4月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量y(箱)与生产时间t(月份)之间的函数图象.| 型号 | A | B |
| 价格(万元/台) | 28 | 25 |
| 日产量(箱/台) | 50 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com