
【题目】
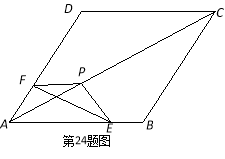
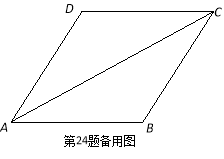
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
⑴求∠EPF的大小;
⑵若AP=8,求AE+AF的值;
⑶若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP长的最大值和最小值.
【答案】(1)120°;(2)![]() ;(3)AP的最大值为12,AP的最小值为6.
;(3)AP的最大值为12,AP的最小值为6.
【解析】
试题分析:(1)如图,过点P作PG⊥EF于G,已知PE=PF=6,EF=![]() ,根据等腰三角形的性质可得FG=EG=
,根据等腰三角形的性质可得FG=EG=![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() .在Rt△FPG中,由sin∠FPG=
.在Rt△FPG中,由sin∠FPG=![]() 可求得∠FPG=60°,所以∠EPF=2∠FPG=120°.(2)作PM⊥AB于M,PN⊥AD于N,根据菱形的性质可得∠DAC=∠BAC,AM=AN,PM=PN,再利用HL证明Rt△PME≌Rt△PNF,即可得NF=ME.又因AP=10,
可求得∠FPG=60°,所以∠EPF=2∠FPG=120°.(2)作PM⊥AB于M,PN⊥AD于N,根据菱形的性质可得∠DAC=∠BAC,AM=AN,PM=PN,再利用HL证明Rt△PME≌Rt△PNF,即可得NF=ME.又因AP=10,![]() ,所以AM= AN =APcos30°=
,所以AM= AN =APcos30°=![]() =
=![]() .所以AE+AF=(AM+ME)+(AN-NF)=AM+AN=
.所以AE+AF=(AM+ME)+(AN-NF)=AM+AN=![]() .(3)如图,当△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动时,点P在
.(3)如图,当△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动时,点P在![]() ,
,![]() 之间运动,易知
之间运动,易知![]() ,
,![]() ,所以AP的最大值为12,AP的最小值为6.
,所以AP的最大值为12,AP的最小值为6.
试题解析:(1)如图,过点P作PG⊥EF于G.
∵PE=PF=6,EF=![]() ,
,
∴FG=EG=![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() .
.
在Rt△FPG中,sin∠FPG=![]() .
.
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°.
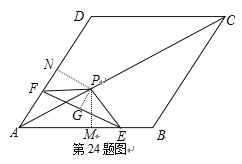
(2)作PM⊥AB于M,PN⊥AD于N.
∵AC为菱形ABCD的对角线,
∴∠DAC=∠BAC,AM=AN,PM=PN.
在Rt△PME和Rt△PNF 中,PM=PN,PE=PF,
∴Rt△PME≌Rt△PNF
∴NF=ME.
又AP=10,![]() ,
,
∴AM= AN =APcos30°=![]() =
=![]() .
.
∴AE+AF=(AM+ME)+(AN-NF)=AM+AN=![]() .
.
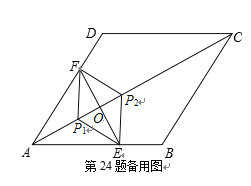
(3) 如图,当△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动时,点P在![]() ,
,![]() 之间运动,易知
之间运动,易知![]() ,
,![]() ,
,
∴AP的最大值为12,AP的最小值为6.


科目:初中数学 来源: 题型:
【题目】四边形的四边顺次为a、b、c、d,且满足a2+b2+c2+d2=2(ab+cd),则这个四边形一定是( )
A.平行四边形
B.两组对角分别相等的四边形
C.对角线互相垂直的四边形
D.对角线长相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( ) 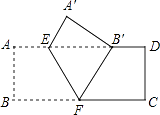
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点. 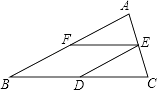
(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( ) 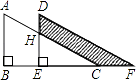
A.20
B.24
C.25
D.26
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com