
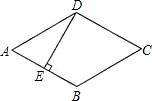
 如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.
如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.
如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
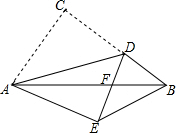 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6月14日晚上能看到月亮 | |
| B. | 早晨的太阳从东方升起 | |
| C. | 打开初三数学书本,正好翻到第21页 | |
| D. | 任意掷一枚均匀的硬币,正面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
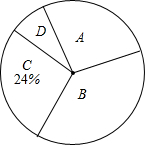 某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
某校课外兴趣小组在本校学生中开展“感动中国2016年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A,B,C,D四类,其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com