【题目】学习了有理数的乘法后，老师给同学们布置这样一道题目：计算49
×（–5），看谁算的又快又对，有三位同学的解法如下：
小军：原式 =（49 + 
）×（–5）= 49×（–5）+ 
×（–5）
=–245–4
=–249
；
小明：原式 = –
× 5 = –
= – 249 
；
小丽：原式 =（49 + 
）×（-5）=（50 -1 + 
）×（-5）
=（50 - 
）×（-5）= 50 ×（-5）+（ - 
） ×（-5）
= –250 +
= –249
；
（1）对于以上三种解法，你认为谁的解法较好？
（2）上面的解法对你有何启发，用你认为最合适的方法计算：
19
×（– 8）
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目：初中数学 来源： 题型：
【题目】几何计算：
如图，已知∠AOB=40°，∠BOC=3∠AOB，OD平分∠AOC，求∠COD的度数．
解：因为∠BOC=3∠AOB，∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=
__________=__________°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于任意四个有理数a，b，c，d，可以组成两个有理数对（a，b）与（c，d）．我们规定：
（a，b）★（c，d）=bc－ad．
例如：（1，2）★（3，4）=2×3－1×4=2．
根据上述规定解决下列问题：
（1）有理数对（2，－3）★（3，－2）=_______；
（2）若有理数对（－3，2x－1）★（1，x+1）=7，则x=_______；
（3）当满足等式（－3，2x－1）★（k，x＋k）=5＋2k的x是整数时，求整数k的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，OE是∠AOD的平分线，OC是∠BOD的平分线．
(1)若∠AOB＝130°，则∠COE是多少度？
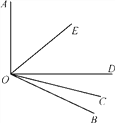
(2)在(1)的条件下，若∠COD＝20°，则∠BOE是多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
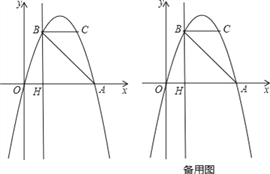
【题目】如图，抛物线y=ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．
（1）求抛物线的表达式；
（2）点P是抛物线上一动点，且位于第四象限，当△ABP的面积为6时，求出点P的坐标；
（3）若点M在直线BH上运动，点N在x轴上运动，当以点C、M、N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC的中点．
（1）求线段MN的长；
（2）若C为线段AB上任一点，满足AC+CB=a cm，其它条件不变，你能猜想MN的长度吗？并说明理由；
（3）若C在线段AB的延长线上，且满足AC﹣BC=b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？并说明理由；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
