6．“双基”考查题（每题2分，共30分）
（1）-27的立方根是-3，18的算术平方根是3$\sqrt{2}$．
（2）化简：$\sqrt{3}×\sqrt{\frac{25}{48}}$=$\frac{5}{4}$，$\sqrt{18}-3\sqrt{32}$=-9$\sqrt{2}$．
（3）比较大小：$\frac{{\sqrt{5}-1}}{2}$＜ $\frac{7}{8}$，$\sqrt{32}$＜5.6．
（4）图象经过点A（-2，6）的正比例函数的关系式为y=-3x．
（5）方程组$\left\{\begin{array}{l}x+2y=7\\ x-2y=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$．
（6）八年级一班47名同学中，12岁的有5人，13岁的有27人，14岁的有12人，15岁的有3人，则这班同学的年龄的众数是13岁，中位数是13岁．
（7）一个正多边形的每个内角都为135°，则这个多边形的内角和是1080度．
（8）将一条2cm线段向右平移3cm后，连接对应点得到的图形的周长是10cm．
（9）、某拖拉机的油箱有油100升，每工作1小时耗油8升，则油箱的剩余油量y（升）与工作时间x（时）间的函数关系式为y=-8x+100．
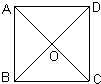
（10）如图，正方形ABCD的对角线相交于点O，这个正方形可以看作由什么“基本图形”经过怎样的变化形成的？Rt△ABC轴对称得到．
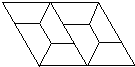
（11）如图是用形状、大小完全相同的等腰梯形密铺成的图案的一部分，这个图案中的等腰梯形的内角度数分别是60°，60°120°，120°．
（12）如图，若用（2，3）表示图上校门A的位置，则图书馆B的位置可表示为（1，6），（5，5）表示点D的位置．
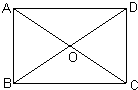
（13）如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB=60°，AB=4cm，则△AOB的形状是等边三角形，AC长是8cm，BC长是4$\sqrt{3}$cm．
（14）小明从九龙山邮局买了面值50分和80分的邮票共9枚，花了6.3元．小明买了两种邮票各多少枚？
若设买了面值50分的邮票x枚，80分的邮票y枚，则可列出的方程组是$\left\{\begin{array}{l}{x+y=9}\\{0.5x+0.8y=6.3}\end{array}\right.$．
（15）根据图填空：
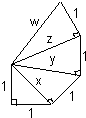
x=$\sqrt{2}$，y=$\sqrt{3}$，z=2，w=$\sqrt{5}$．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
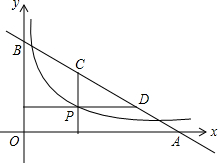如图，P是函数y=$\frac{\sqrt{3}}{x}$（x＞0）图象上的一点，直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴、y轴别交于A，B两点，过P作x轴、y轴的垂线与该直线分别交于C，D两点，则AD•BC=4．
