
【题目】问题:探究函数y=|x|-1的性质.
小凡同学根据学习函数的经验,对函数y=|x|-1的图象与性质进行了探究.下面是小凡的探究过程,请补充完整:
(1)在函数y=|x|-1中,自变量x的取值范围是______________;
(2)下表是y与x的几组对应值.
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||
y | 2 | 1 | 0 | -1 | 0 | 1 | m |
①m=_________;
②若A(n,9),B(10,9)为该函数图象上不同的两点,则_n=__________;
(3)如下图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;

(4)结合函数图象,解决问题:
①函数的最小值为________;
②已知直线![]() 与函数
与函数![]() 的图象交于C,D两点,当y1≥y时x的取值范围是___________.
的图象交于C,D两点,当y1≥y时x的取值范围是___________.
【答案】(1)全体实数(或任意实数) (2)①2 ②-10 (3)作图见解析 (4)①-1 ②![]()
【解析】
(1)根据函数和图象的性质,写出自变量x的取值范围即可;
(2)①根据函数解析式求出m的值即可;②根据函数解析式求出n的值即可;
(3)利用描点法作出图象即可;
(4)①根据图象求出最小值即可;②分情况讨论:1)当![]() 时,2)当
时,2)当![]() 时,分别列不等式求解即可.
时,分别列不等式求解即可.
(1)根据函数和图象的性质可得,自变量x的取值范围是全体实数(或任意实数);
(2)①令![]() ,则
,则![]() ;
;
②∵A(n,9),B(10,9)为该函数图象上不同的两点
∴![]() 且
且![]()
解得![]() ;
;
(3)如图所示,即为所求;

(4)①如图所示,当![]() 时,函数有最小值,最小值为-1;
时,函数有最小值,最小值为-1;
②1)当![]() 时,
时,
∵![]()
∴![]()
解得![]()
∴![]()
2)当![]() 时,
时,
∵![]()
∴![]()
解得![]()
∴![]()
综上所述,![]() .
.


科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
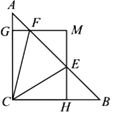
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对边相等目这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”.
(1)如图①,四边形![]() 与四边形
与四边形![]() 都是正方形,
都是正方形,![]() ,求证:四边形
,求证:四边形![]() 是“等垂四边形”;
是“等垂四边形”;
(2)如图②,四边形![]() 是“等垂四边形”,
是“等垂四边形”,![]() ,连接
,连接![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是AD,BC,BD的中点,连接EG,FG,EF.试判定
分别是AD,BC,BD的中点,连接EG,FG,EF.试判定![]() 的形状,并证明;
的形状,并证明;
(3)如图③,四边形![]() 是“等垂四边形”,
是“等垂四边形”,![]() ,
,![]() ,试求边AB长的最小值.
,试求边AB长的最小值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
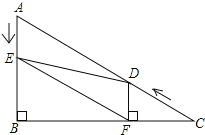
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
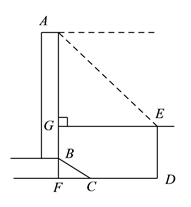
【题目】如图所示,某办公大楼正前方有一根高度是![]() 米的旗杆
米的旗杆![]() ,从办公楼顶端
,从办公楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是
是![]() ,旗杆底端
,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是
是![]() 米,梯坎坡长
米,梯坎坡长![]() 是
是![]() 米,梯坎坡度
米,梯坎坡度![]() ,求大楼
,求大楼![]() 的高度.(精确到
的高度.(精确到![]() 米,参与数据:
米,参与数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() 的顶点坐标为:
的顶点坐标为:![]() ,
,![]() ,
,![]() .
.
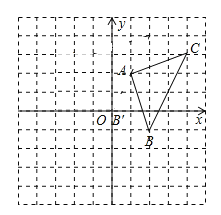
(1)将![]() 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得![]() .画出
.画出![]() 并写出
并写出![]() 的顶点坐标;
的顶点坐标;
(2)请判断![]() 的形状并求它的面积.
的形状并求它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成。
(1)若围成的面积为180m2,试求出自行车车棚的长和宽;
(2)能围成的面积为200m2自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com