
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点C,交AB的延长线于点E,连接CD、CE.
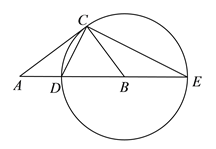
(1)求证:△ACD∽△AEC;
(2)当![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4![]() ,求△ACE的面积.
,求△ACE的面积.
【答案】(1)证明见解析(2)![]() (3)12
(3)12![]()
【解析】试题分析:(1)、根据直径所对的圆周角为直角以及BC=CE得出∠ACD=∠E,然后根据∠A为公共角得出三角形相似;(2)、设AC=4k,则BC=3k,则AE=8k,根据三角形相似得出tanE=![]() =
=![]() 得出答案;(3)、过点E作EH⊥AC,垂足为H.设⊙B的半径为R,根据Rt△ABC的勾股定理得出R的值,然后根据△ABC∽△AEH得出EH的长度,从而求出△ACE的面积.
得出答案;(3)、过点E作EH⊥AC,垂足为H.设⊙B的半径为R,根据Rt△ABC的勾股定理得出R的值,然后根据△ABC∽△AEH得出EH的长度,从而求出△ACE的面积.
试题解析:(1)∵DE为⊙B的直径,
∴∠DCE=90°,
∵∠ACB=90°,∠ACD=∠BCE.
∵BC=CE,
∴∠BCE=∠E,
∴∠ACD=∠E,
又∵∠CAD=∠EAC,
∴△ACD∽△AEC;
(2)∵![]() ,
,
设AC=4k,则BC=3k,
∴在Rt△ABC中,AB=5k,BD=3k,AE=AB+BE=8k.
由(1)知:△DCE为直角三角形,
则tanE=![]() .
.
∵△ACD∽△AEC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
即tanE=![]() =
=![]() ;
;
(3)过点E作EH⊥AC,垂足为H.设⊙B的半径为R.
∵在Rt△ABC中,∠ACB=90°,
∴AB2=AC2+BC2,
∴(4+R)2=(4![]() )2+R2,
)2+R2,
解得R=4.
即BC=4,DE=2BC=8,AB=8,AE=12.
∵∠ACB=∠AHE=90°,∠CAB=∠CAE,
∴△ABC∽△AEH,
∴![]() ,
,
即![]() ,
,
解得EH=6,
∴△ACE的面积为![]() AC·EH=
AC·EH=![]() ×4
×4![]() ×6=12
×6=12![]()


科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
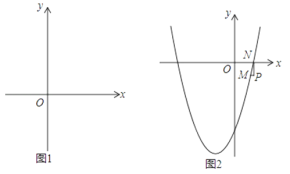
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便行人过马路,打算修建一座高为4x(m)的过街天桥.已知天桥的斜面坡度i=1:0.75是指坡面的铅直高度DE(CF)与水平宽度AE(BF)的比,其中DC∥AB,CD=8x(m).
(1)请求出天桥总长和马路宽度AB的比;
(2)若某人从A地出发,横过马路直行(A→E→F→B)到达B地,平均速度是2.5m/s;返回时从天桥由BC→CD→DA到达A地,平均速度是1.5m/s,结果比去时多用了12.8s,请求出马路宽度AB的长.
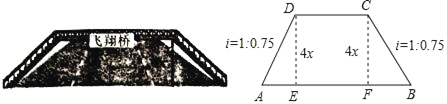
查看答案和解析>>
科目:初中数学 来源: 题型:
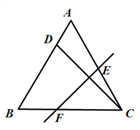
【题目】已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、
F分别在AC和BC上.如图,若AD∶DB=1∶4,则CE∶CF=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字-1、-2、0;先从甲袋中随机取出一个小球,记录标有的数字为x,再从乙袋中随机取出一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x2-1的图象上的概率;
(3)若以点M为圆心,2为半径作⊙M,求⊙M与坐标轴相切的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com