
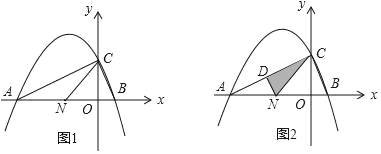
【题目】如图1,抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣![]() ,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
(1)求出抛物线的解析式,并写出C点的坐标;
(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.
(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2,C(0,2);(2)当n=2
x+2,C(0,2);(2)当n=2![]() ﹣4或﹣
﹣4或﹣![]() 时,△ANC是等腰三角形;(3)当n=﹣
时,△ANC是等腰三角形;(3)当n=﹣![]() 时,△DCN的面积最大,最大值为
时,△DCN的面积最大,最大值为![]() .
.
【解析】
(1)由抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣![]() (x+4)(x﹣1),由此即可解决问题;
(x+4)(x﹣1),由此即可解决问题;
(2)分别表示出AC、AN、NC,然后分三种情形讨论:①当AN=AC时;②当NA=NC时,③当NC=AC时;分别构建方程即可解决问题;
(3)根据S△CDN=S△ANC﹣S△ADN构建二次函数,利用二次函数的性质解决最值问题;
(1)∵抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,不妨设抛物线的解析式为y=﹣![]() (x+4)(x﹣1),即y=﹣
(x+4)(x﹣1),即y=﹣![]() x2﹣
x2﹣![]() x+2,∴C(0,2).
x+2,∴C(0,2).
(2)∵A(﹣4,0),N(n,0),C(0,2),∴AC=![]() =2
=2![]() ,AN= n+4,NC=
,AN= n+4,NC=![]() .
.
分三种情况讨论:
①当AN=AC时,n+4=2![]() ,解得:n=2
,解得:n=2![]() ﹣4.
﹣4.
②当NA=NC时,n+4=![]() ,解得:n=﹣
,解得:n=﹣![]() .
.
③当NC=AC时,![]() =2
=2![]() ,解得:n=±4.
,解得:n=±4.
∵点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),故这种情况不成立.
综上所述:当n=2![]() ﹣4或﹣
﹣4或﹣![]() 时,△ANC是等腰三角形.
时,△ANC是等腰三角形.
(3)由题意可知:直线BC的解析式为y=﹣2x+2,直线AC的解析式为y=![]() x+2,设N(n,0).
x+2,设N(n,0).
∵ND∥BC,设ND的解析式为y=﹣2x+b,代入(n,0)可得:b=2n,∴ND的解析式为y=﹣2x+2n,由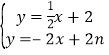 ,可得点D的纵坐标:yD=
,可得点D的纵坐标:yD=![]() (8+2n),∴S△CDN=S△ANC﹣S△ADN =
(8+2n),∴S△CDN=S△ANC﹣S△ADN =![]() [2×(n+4)﹣
[2×(n+4)﹣![]() (8+2n)(n+4)]=
(8+2n)(n+4)]=![]() =﹣
=﹣![]() (n+
(n+![]() )2+
)2+![]() .
.
∵﹣![]() <0,∴当n=﹣
<0,∴当n=﹣![]() 时,△DCN的面积最大,最大值为
时,△DCN的面积最大,最大值为![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
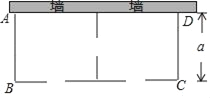
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.

请回答:这样做的依据是__________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
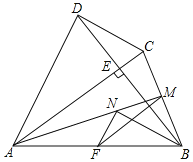
【题目】如图,四边形ABCD中,AC⊥BD交BD于点E,点F、M分别是AB、BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF
求证:(1)BN=![]() MN;
MN;
(2)△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
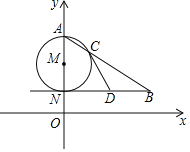
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
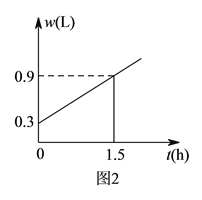
【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水![]() 与滴水时间
与滴水时间![]() 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图![]() 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图![]() 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.
(![]() )容器内原有水多少升.
)容器内原有水多少升.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.

查看答案和解析>>
科目:初中数学 来源: 题型:
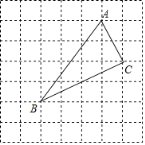
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )

A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C.小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
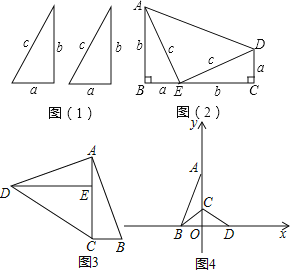
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形构造图3的图形,你能利用这个图形证明出题(1)的结论吗?如果能,请写出证明过程;
(3)当a=3,b=4时,将其中一个直角三角形放入平面直角坐标系中,使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合(如图4中Rt△AOB的位置).点C为线段OA上一点,将△ABC沿着直线BC翻折,点A恰好落在x轴上的D处.
①请写出C、D两点的坐标;
②若△CMD为等腰三角形,点M在x轴上,请直接写出符合条件的所有点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com