
 .其中正确的是( )
.其中正确的是( )
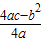 =3,
=3, )2-4×
)2-4×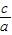 =
= ,
, =3,
=3, =-12,
=-12,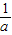 ×(-12)=
×(-12)=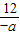 ,
,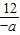 =32=9,
=32=9, ,故④正确;
,故④正确;

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
 C′时,抛物线在x轴上截得的线段长为6,求点C′的坐标.
C′时,抛物线在x轴上截得的线段长为6,求点C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
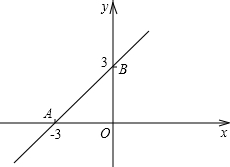
 (2012•龙岩质检)在平面直角坐标系中,ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),
(2012•龙岩质检)在平面直角坐标系中,ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),查看答案和解析>>
科目:初中数学 来源: 题型:
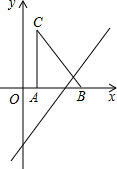 (2012•唐山二模)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为
(2012•唐山二模)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(4,0)、(4,3),动点M、N分别从点O、B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,当两动点运动了t秒时.解答下列问题:
如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(4,0)、(4,3),动点M、N分别从点O、B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,当两动点运动了t秒时.解答下列问题:| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
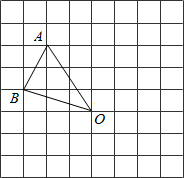 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com