
����Ŀ����ʤ�ذ�ƺ������������ζȼٴ�Ⱥ����⾰����֯![]() ������װ����
������װ����![]() ������ȹ�
������ȹ�![]() �ֵ��������.���ƻ���
�ֵ��������.���ƻ���![]() ��������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ����ȣ��ұ���װ��.�����±��ṩ����Ϣ������������⣺
��������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ����ȣ��ұ���װ��.�����±��ṩ����Ϣ������������⣺
���Ʒ�� |
|
|
|
ÿ���������������֣� |
|
|
|
ÿ����Ȼ�ã�Ԫ�� |
|
|
|
![]() ��װ��
��װ��![]() ����ȵij�����Ϊ
����ȵij�����Ϊ![]() ��װ��
��װ��![]() ����ȵij�����Ϊ
����ȵij�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
![]() ���װ��ÿ����ȵij�������������
���װ��ÿ����ȵij�������������![]() ������ô�����İ��ŷ����м��֣�
������ô�����İ��ŷ����м��֣�
![]() ����������Ϊ
����������Ϊ![]() ��Ԫ������
��Ԫ������![]() ��
��![]() ֮��ĺ�����ϵʽ����Ҫʹ�˴����ۻ������Ӧ�������ְ��ŷ������������������ֵ.
֮��ĺ�����ϵʽ����Ҫʹ�˴����ۻ������Ӧ�������ְ��ŷ������������������ֵ.
���𰸡���1��![]() ����2��5�֣���3��װ��
����2��5�֣���3��װ��![]() �����
�����![]() ����
����![]() �����
�����![]() ����
����![]() �����
�����![]() ��ʱ����������������Ϊ
��ʱ����������������Ϊ![]() Ԫ.
Ԫ.
��������
(1)���á�������֮��=20�����������ϵ������ʽ���ɣ�
(2)��ϵʽΪ��װ��ÿ����ȵij�������4��
(3)������Ϊ��װ��A����ȵij�������6��1200+װ��B����ȵij�������5��1600+װ��C����ȵij�������4��1000��Ȼ��x��ȡֵ���ж���
�⣺��1���������⣬װ��![]() ����ȵij�����Ϊ
����ȵij�����Ϊ![]() ��װ��
��װ��![]() ����ȵij�����Ϊ
����ȵij�����Ϊ![]() ����ôװ��
����ôװ��![]() ����ȵij�����Ϊ
����ȵij�����Ϊ![]() ��
��
����![]() ������
������![]()
��2����![]() ֪��װ��
֪��װ��![]() ������ȵij������ֱ�Ϊ
������ȵij������ֱ�Ϊ![]()
������ã�![]()
���![]() ��
��
��Ϊ![]() Ϊ������
������
����![]() ��ֵΪ
��ֵΪ![]() �������ŷ�������
�������ŷ�������![]() ��.
��.
��3��![]()
![]()
![]() ��ֵ��
��ֵ��![]() ���������С
���������С
Ҫʹ![]() ���������
���������![]() ��
��
��ѡ����Ϊ��װ��![]() �����
�����![]() ����
����![]() �����
�����![]() ����
����![]() �����
�����![]() ��.
��.
![]() ��Ԫ��
��Ԫ��
�𣺵�װ��![]() �����
�����![]() ����
����![]() �����
�����![]() ����
����![]() �����
�����![]() ��ʱ����������������Ϊ
��ʱ����������������Ϊ![]() Ԫ.
Ԫ.
�ʴ�Ϊ����1��![]() ����2��5�֣���3��װ��
����2��5�֣���3��װ��![]() �����
�����![]() ����
����![]() �����
�����![]() ����
����![]() �����
�����![]() ��ʱ����������������Ϊ
��ʱ����������������Ϊ![]() Ԫ.
Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y��ax2+2ax+c��y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣮��B������Ϊ��1��0����OC��3OB��
��1���������ߵĽ���ʽ��
��2����a��0ʱ����ͼ��ʾ������D�ǵ��������������ϵĶ��㣬���D�ĺ�����Ϊm��������ADC�����ΪS�����S��m�ĺ�����ϵʽ����ֱ��д���Ա���m��ȡֵ��Χ�����ʵ�mΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���е㡣������
���е㡣������![]() ������ȡһ��
������ȡһ��![]() ������
������![]() ,���߶�
,���߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת80�㣬��
��ʱ�뷽����ת80�㣬��![]() �Ķ�Ӧ���ǵ�
�Ķ�Ӧ���ǵ�![]() ������
������![]() .
.
��1����ͼ1������![]() ��������
��������![]() ��ʱ��
��ʱ��
��![]() _________________����
_________________����
��ֱ��![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ��______________________��
��λ�ù�ϵ��______________________��

��2����ͼ2������![]() ��������
��������![]() �����ʱ�����ж�ֱ��
�����ʱ�����ж�ֱ��![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ����֤����Ľ��ۡ�
��λ�ù�ϵ����֤����Ľ��ۡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ե�P��-1,0��ΪԲ�ĵ�Բ����x����B��C���㣨B��C����ࣩ����y����A��D���㣨A��D���·�����AD=![]() ������ABC�Ƶ�P��ת180�����õ���MCB��
������ABC�Ƶ�P��ת180�����õ���MCB��

��1����B��C��������ꣻ
��2������ͼ�л����߶�MB��MC�����ж��ı���ACMB����״������֤�����������M�����ꣻ
��3����ֱ��l����BM�غϵ�λ�ÿ�ʼ�Ƶ�B˳ʱ����ת������BC�غ�ʱֹͣ����ֱ��l��CM����ΪE����QΪBE���е㣬����E��EG��BC��G������MQ��QG����������ת�����С�MQG�Ĵ�С�Ƿ�仯�������䣬�����MQG�Ķ��������仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���ABC�͡�DEF���ƣ������λ�����������Ʊ�������ȷ���ǣ�������

A. λ�������ǵ�B�����Ʊ���2��1 B. λ�������ǵ�D�����Ʊ���2��1
C. λ�������ڵ�G��H֮�䣬���Ʊ�Ϊ2��1 D. λ�������ڵ�G��H֮�䣬���Ʊ�Ϊ1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ��A��ǰ�����5ǧ��B�أ��������г���;����������20���ӣ�����ʻ��·��s��ǧ�ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ�����������е�·��s��ǧ�ף�����ʱ��t�����ӣ��ĺ�������ʽΪ![]()
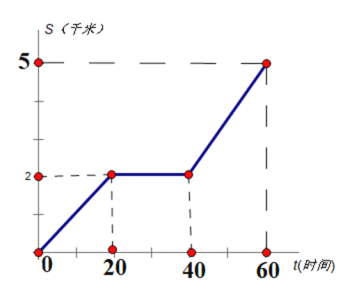
��1����ͼ�л������������е�·�̹���ʱ��ĺ���ͼ��
��2����������ʻ���ٶ���ÿ����_______��;
��3���ס��������ڳ�������;_________����ʱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABO�Ķ���A�Ƿ���������y=![]() ��һ�κ���y=��x����k+1����ͼ���ڵڶ����Ľ��㣬AB��x����B����S��ABO=
��һ�κ���y=��x����k+1����ͼ���ڵڶ����Ľ��㣬AB��x����B����S��ABO=![]() ��
��
��1��ֱ��д�������������Ĺ�ϵʽ��
��2�����AOC�������
��3������ͼ��ֱ��д������xΪ��ֵʱ��������������ֵС��һ�κ�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=2AC, ��D��BC�ϣ��ҡ�CAD=��B����E��AB���е㣬����CE��AD���ڵ�G,��F��BC�ϣ��ҡ�CEF=��BAC.
(1)����BAC=90��,��ͼ1,��֤: EG+ EF=![]() AC;
AC;
(2)����BAC=120��,��ͼ2,������߶�EG��EF��AC֮���������ϵ��֤��.
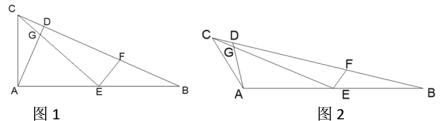
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com