
分析 首先对x和y的值进行分母有理化,(1)把化简后的x和y的值代入计算即可;
(2)把所求的式子化成(x+y)2-3xy的形式,然后根据(1)的结果计算即可.
解答 解:x=$\frac{1}{\sqrt{2}-1}$=$\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}$=$\sqrt{2}$+1,y=$\frac{1}{1+\sqrt{2}}$=$\frac{\sqrt{2}-1}{(1+\sqrt{2})(\sqrt{2}-1)}$=$\sqrt{2}$-1.
(1)x+y=($\sqrt{2}$+1)+($\sqrt{2}$-1)=2$\sqrt{2}$,
xy=($\sqrt{2}$+1)($\sqrt{2}$-1)=2-1=1;
(2)原式=(x+y)2-3xy=(2$\sqrt{2}$)2-3×1=8-3=5.
点评 本题考查了二次根式的化简求值,正确进行分母有理化是关键.


科目:初中数学 来源: 题型:选择题
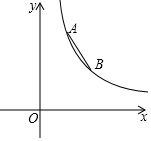 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,且AB=$\sqrt{13}$.则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有A、B两点,A点的横坐标为2,B点的横坐标为4,且AB=$\sqrt{13}$.则k的值为( )| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com