
【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
【答案】B
【解析】
过P作BC的平行线,交AC于M;则△APM也是等边三角形,在等边三角形APM中,PE是AM上的高,根据等边三角形三线合一的性质知AE=EM;易证得△PMD≌△QCD,则DM=CD;此时发现DE的长正好是AC的一半,由此得解.
解答:解:过P作PM∥BC,交AC于M;

∵△ABC是等边三角形,且PM∥BC,
∴△APM是等边三角形;
又∵PE⊥AM,
∴AE=EM=![]() AM;(等边三角形三线合一)
AM;(等边三角形三线合一)
∵PM∥CQ,
∴∠PMD=∠QCD,∠MPD=∠Q;
又∵PA=PM=CQ,
∴△PMD≌△QCD(ASA);
∴CD=DM=![]() CM;
CM;
∴DE=DM+ME=![]() (AM+MC)=
(AM+MC)=![]() AC=
AC=![]() ,故选B.
,故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过点C. 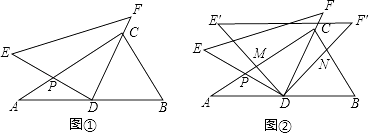
(1)求∠ADE的度数;
(2)如图②,在图①的基础上将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( ) 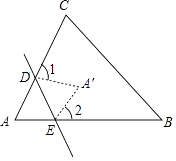
A.α
B.2α
C.180°﹣α
D.180°﹣2α
查看答案和解析>>
科目:初中数学 来源: 题型:
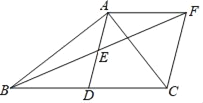
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的情况下,点M在AC线段上移动,请直接回答,当点M移动到什么位置时,MB+MD有最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国国家邮政局公布的数据显示,2016年中国快递业务量突破313.5亿件,同比增长51.7%,快递业务量位居世界第一,业内人士表示,快递业务连续6年保持50%以上的高速增长,已成为中国经济的一匹“黑马”,未来中国快递业务仍将保持快速增长势头,以下是根据相关数据绘制的统计图,请你预估2017年全国快递的业务量大约为(精确的0.1)亿元. 
查看答案和解析>>
科目:初中数学 来源: 题型:
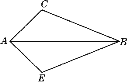
【题目】如图,对角线AB把四边形ACBE分为△ABC和△ABE两部分,如果△ABC中BC边上的高和△ABE中BE边上的高相等,且AC=AE.
(1)在原图上画出△ABC中BC边上的高AD与△ABE中BE边上的高AF;
(2)请你猜想BC与BE的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4) 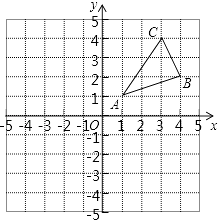 .
.
(1)请画出△ABC关于原点对称的△A2B2C2;并写出各点的坐标.
(2)在x轴上求作一点P,使△PAB的周小最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com