
【题目】问题提出:
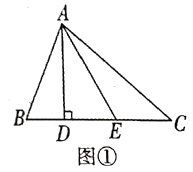
(1)如图①在![]() 中,
中,![]() 是
是![]() 边
边![]() 的高,点
的高,点![]() 是
是![]() 上任意一点,若
上任意一点,若![]() 则
则![]() 的最小值为_ ;
的最小值为_ ;
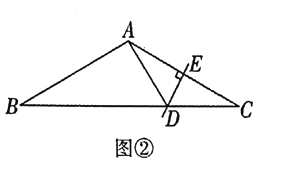
(2)如图②,在等腰![]() 中,
中,![]() 是
是![]() 的垂直平分线,分别交
的垂直平分线,分别交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
问题解决:
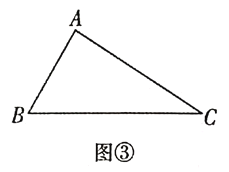
(3)如图③,某公园管理员拟在园内规划一个![]() 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路
区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路![]() 和
和![]() ,满足
,满足![]() 点
点![]() 到
到![]() 的距离为
的距离为![]() .为了节约成本,要使得
.为了节约成本,要使得![]() 之和最短,试求
之和最短,试求![]() 的最小值(路宽忽略不计).
的最小值(路宽忽略不计).
【答案】(1)3;(2)![]() ;(3)
;(3)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)根据直线外一点与直线上的点的所有连线中,垂线段最短即可求解;
(2)由已知和等腰三角形的性质得出![]() ,根据垂直平分线的性质和含30度角的直角三角形的性质可依次得出
,根据垂直平分线的性质和含30度角的直角三角形的性质可依次得出![]() ,
,![]() ,利用勾股定理求出AB,即可求得
,利用勾股定理求出AB,即可求得![]() 的周长;
的周长;
(3)延长![]() 到点
到点![]() ,使得
,使得![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,则
,则![]() 的最小值即为
的最小值即为![]() 的最小值;通过角的计算可得
的最小值;通过角的计算可得![]() ,可得点
,可得点![]() 在弦
在弦![]() 所对的劣弧上;过点
所对的劣弧上;过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
由![]() 即可求得结果.
即可求得结果.
解:(1)∵![]() 是
是![]() 边
边![]() 的高,
的高,![]() ,
,
∴![]() ,点D到直线BC的距离为3,
,点D到直线BC的距离为3,
∵点![]() 是
是![]() 上任意一点,
上任意一点,
∴![]() ,即
,即![]() ,
,
∴![]() 的最小值为3,
的最小值为3,
故答案为:3.
(2)![]() ,
,
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的周长
的周长![]() ;
;
(3)如图,延长![]() 到点
到点![]() ,使得
,使得![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 的最小值即为
的最小值即为![]() 的最小值,
的最小值,
![]()
![]() ,
,
以![]() 为斜边向下作等腰直角三角形
为斜边向下作等腰直角三角形![]() ,则
,则![]() ,
,
以点![]() 为圆心
为圆心![]() 为半径作
为半径作![]() ,F为圆上任意一点,则
,F为圆上任意一点,则![]() ,
,
∵![]() ,
,
![]() 点
点![]() 在弦
在弦![]() 所对的劣弧上,
所对的劣弧上,
如图,过点![]() 作
作![]() 于
于![]() 过点
过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() ,
,
设![]() 则
则![]()
则![]() ,即
,即![]()
解得:![]() ,则
,则![]() ,
,
![]() 的最小值为
的最小值为![]() ,
,
![]() 的最小值为
的最小值为![]() .
.



科目:初中数学 来源: 题型:
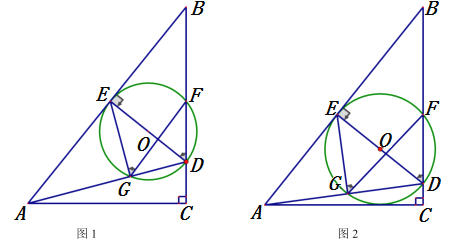
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一个动点,作
上一个动点,作![]() ,交直角边
,交直角边![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .连结
.连结![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)求证:![]() ;
;
(3)如图2,当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的直径;
的直径;
(4)若以![]() 为顶点的三角形是等腰三角形时,求所有满足条件的
为顶点的三角形是等腰三角形时,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
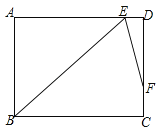
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
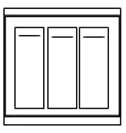
【题目】小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮).
(1)若小惠任意闭合一个开关,“客厅灯亮了”是_______事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是_______事件(填“不可能”或“必然”或“随机”);
(2)若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
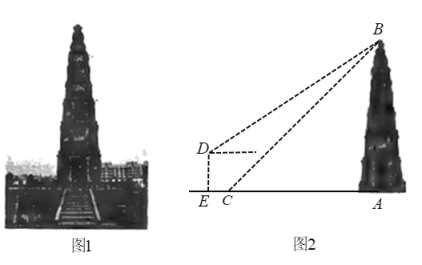
【题目】如图1,在唐河县文峰广场,耸立着一座古老建筑-文峰塔,传说唐河县城是一个船地, 唐中是船头,文峰塔是船的桅杆,无论唐河水怎么涨,唐河县城这艘船也水涨船高.学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量文峰塔的高度.如图2,刘明在点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() 王华在高台上的点
王华在高台上的点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() ,若高台
,若高台![]() 高为
高为![]() 米,点
米,点![]() 到点
到点![]() 的水平距离EC为
的水平距离EC为![]() 米,且
米,且![]() 三点共线,求该塔
三点共线,求该塔![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,结果保留整数)
,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
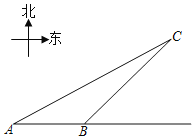
【题目】如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
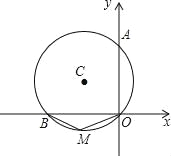
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
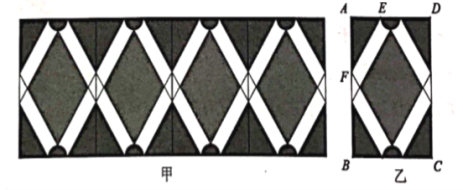
【题目】图甲是小明设计的花边图案作品该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).该矩形图案既是轴对称图形,又是中心对称图形.图乙中,![]() ,上、下两个半圆的面积之和为
,上、下两个半圆的面积之和为![]() ,中间阴影菱形的一组对边与
,中间阴影菱形的一组对边与![]() 平行,且菱形的面积比
平行,且菱形的面积比![]() 个角上的阴影三角形的面积之和大
个角上的阴影三角形的面积之和大![]() ,则
,则![]() 的长度为__________
的长度为__________![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com