

分析 (1)先判断出AD是BC的垂直平分线,即可得出结论;
(2)先判断出等腰三角形AEF的腰,再用等腰三角形的性质和三角形的外角的性质即可得出结论;
(3)先判断出,∠AFE=BGE,进而构造出全等三角形,即可得出结论.
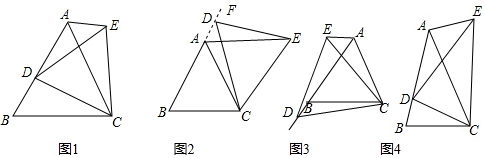
解答 解: (1)∵AD是等边△ABC的高,
(1)∵AD是等边△ABC的高,
∴AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE,
(2)∵AD是等边△ABC的高,
∴∠CAD=$\frac{1}{2}$∠BAC=30°,
∴△AEF为等腰三角形,
∴腰为AE或AF,AE=AF,
∴∠AEF=∠AFE=75°,
∵∠ACB=60°,
∴∠CBF=∠AFE-∠ACB=75°-60°=15°,
∵BE=CE,
∴∠ECD=∠CBF=15°,
故答案为AE或AF
(3)EF=EG,
理由:∵∠BAC=60°,∠FEG=120°,
∴∠BAC+∠FEG=180°,
∴∠AGE+∠AFE=180°,
∴∠AFE=BGE,
过点E作EN⊥AB,EM⊥AC,
∵AD是∠BAC的平分线,
∴EN=EM;
在△ENG和△EMF中,$\left\{\begin{array}{l}{∠EGN=∠EFM}\\{∠ENG=∠EMF=90°}\\{EN=EM}\end{array}\right.$,
∴△ENG≌△EMF,
∴EG=EF
点评 此题是三角形综合题,主要考查了等边三角形的性质,等腰三角形的性质,垂直平分线的性质和判定,全等三角形的判定,解本题的关键是掌握等边三角形的性质,是一道比较简单的中考常考题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-5x+4=0 | B. | 3x2-5x+4=0 | C. | x2+2x+4=0 | D. | x2-5x+4=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 几个有理数相乘,当负因数有奇数个时积为负 | |
| B. | 倒数等于它本身的数是+1 | |
| C. | 一个有理数的相反数一定是负有理数 | |
| D. | -1乘以任何有理数,都等于这个有理数的相反数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
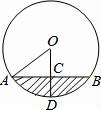 如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,求(1)水的最大深度CD(2)若角AOD为50度,求阴影部分的面积.
如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,求(1)水的最大深度CD(2)若角AOD为50度,求阴影部分的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com