
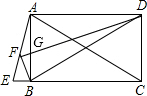
 已知四边形ABCD为矩形,延长CB到E,使CE=CA,连接AE,F为AE的中点,连接BF,DF,DF交AB于点G,下列结论:
已知四边形ABCD为矩形,延长CB到E,使CE=CA,连接AE,F为AE的中点,连接BF,DF,DF交AB于点G,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 方法一、利用矩形的性质和直角三角形的性质得出结论判断出△BDF≌△ACF,借助直角三角形的斜边大于直角边,再用面积公式判断出面积大小,判断出△AFG∽△DFA,△BFG∽△DFB,即可判断出结论.
方法二、利用矩形的性质和直角三角形的性质得出结论判断出△BDF≌△ACF,进而判断出B、F、A、D四点共圆.
解答 解:方法一、如图1,连接CF,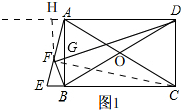
设AC与BD的交点为点O,
∵点F是AE中点,
∴AF=EF,
∵CE=CA,
∴CF⊥AE,
∵四边形ABCD是矩形,
∴AC=BD,
∴OA=OB,
∴∠OAB=∠OBA,
∵点F是Rt△ABE斜边上的中点,
∴AF=BF,
∴∠BAF=∠FBA,
∴∠FAC=∠FBD,
在△BDF和△ACF中,$\left\{\begin{array}{l}{AF=BF}\\{∠FAC=∠FBD}\\{AC=BD}\end{array}\right.$,
∴△BDF≌△ACF,
∴∠BFD=∠AFC=90°,
∴BF⊥DF,
所以①正确;
过点F作FH⊥AD交DA的延长线于点H,
在Rt△AFH中,FH<AF,
在Rt△BFG中,BG>BF,
∵AF=BF,
∴BG>FH,
∵S△ADF=$\frac{1}{2}$FH×AD,S△BDG=$\frac{1}{2}$BG×AD,
∴S△BDG>S△ADF,
所以②错误;
∵∠ABF+∠BGF=∠ADG+∠AGD=90°,
∴∠ABF=∠ADG,
∵∠BAF=∠FBA,
∴∠BAF=∠ADG,
∵∠AFG=∠DFA,
∴△AFG∽△DFA,
∴$\frac{AF}{FD}=\frac{FG}{AF}$,
∴AF2=FG•FD,
∵EF=AF,
∴EF2=FG•FD,
所以③正确;
∵BF=EF,
∴BF2=FG•FD,
∴$\frac{BF}{FG}=\frac{FD}{BF}$,
∵∠BFG=∠DFB,
∴△BFG∽△DFB,
∴∠ABF=∠BDF,
∵由③知,∠ABF=∠ADF
∴∠ADF=∠BDF,
∴$\frac{AG}{BG}=\frac{AD}{BD}$(利用角平分线定理),
∵BD=AC,AD=BC,
∴$\frac{AG}{BG}=\frac{BC}{AC}$,
所以④正确,
故选C.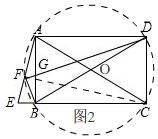 方法二、连接CF,
方法二、连接CF,
设AC与BD的交点为点O,
∵点F是AE中点,
∴AF=EF,
∵CE=CA,
∴CF⊥AE,
∵四边形ABCD是矩形,
∴AC=BD,
∴OA=OB,
∴∠OAB=∠OBA,
∵点F是Rt△ABE斜边上的中点,
∴AF=BF,
∴∠BAF=∠FBA,
∴∠FAC=∠FBD,
在△BDF和△ACF中,$\left\{\begin{array}{l}{AF=BF}\\{∠FAC=∠FBD}\\{AC=BD}\end{array}\right.$,
∴△BDF≌△ACF,
∴∠BFD=∠AFC=90°,
∴BF⊥DF,所以①正确;
∴∠BFD=∠BAD=90°,
∴点B、F、A、D四点在以BD为直径的圆上,
∵点F是直角三角形ABE的斜边AE的中点,
∴BF=AF=EF,
∴∠ADF=∠BDF,
∴S△ADF=S△BDF,
∵S△BDG<S△BDF,
∴S△ADF>S△BDG,∴②错误;
∵∠ADF=∠BDF,∠ADF=∠BDF,
∴∠AFG=∠AFG,
∴△AFG∽△DFA,
∴∴$\frac{AF}{FD}=\frac{FG}{AF}$,
∴AF2=FG•FD,
∵EF=AF,
∴EF2=FG•FD,
所以③正确;
∵∠ADF=∠BDF,
∴$\frac{AG}{BG}=\frac{AD}{BD}$(利用角平分线定理),
∵BD=AC,AD=BC,
∴$\frac{AG}{BG}=\frac{BC}{AC}$,
所以④正确,
故选C.
附:角平分线定理:
如图,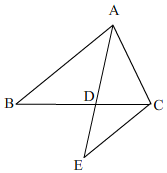
∵AD是∠BAC的角平分线交BC于D,
∴∠BAD=∠CAD,
过点C作CE∥AB交AD的延长线于E,
∴∠BAD=∠E,
∴∠CAD=∠E,
∴AC=CE,
∵∠BAD=∠E,∠ADB=∠EDC,
∴△ABD∽△ECD,
∴$\frac{AB}{CE}=\frac{BD}{CD}$,
∴$\frac{AB}{AC}=\frac{BD}{CD}$.
点评 此题是相似三角形的性质和判定,全等三角形的判定和性质,直角三角形的性质,等腰三角形的性质,三角形内角平分线定理,解本题的是△BDF≌△ACF.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲、乙射中的总环数相同 | B. | 甲的成绩稳定 | ||
| C. | 乙的成绩波动较大 | D. | 甲、乙的众数相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
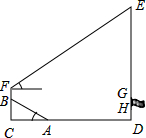 某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).
某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com