
【题目】甲、乙两列火车分别从![]() ,
,![]() 两城同时匀速驶出,甲车开往
两城同时匀速驶出,甲车开往![]() 城,乙车开往
城,乙车开往![]() 城.由于墨迹遮盖,图中提供的只是两车距
城.由于墨迹遮盖,图中提供的只是两车距![]() 城的路程
城的路程![]() (千米),
(千米),![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数图象的一部分.
(时)的函数图象的一部分.
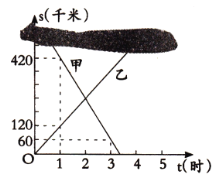
(1)乙车的速度为_______________千米![]() 时;
时;
(2)分别求出![]() ,
,![]() 与
与![]() 的函数解析式(不必写出
的函数解析式(不必写出![]() 的取值范围);
的取值范围);
(3)求出两城之间的路程,及![]() 为何值时两车相遇;
为何值时两车相遇;
(4)当两车相距![]() 千米时,求
千米时,求![]() 的值.
的值.
【答案】(1)120;(2)s甲=-180t+600;s乙=120t; (3)600千米; t=2;(4)t的值为1或3.
【解析】
(1)根据图像可知,当t=1时,S=120,故![]()
![]() =120(千米/时).
=120(千米/时).
(2)S甲过点(3,60)和点(1,420),将点(3,60)和点(1,420)代入解析式利用待定系数法求得k、b值,从而求得S甲的关系式,同理求得正比例函数S乙的关系式.
(3)当t=0时,求得S甲的值,此时S甲的值表示两城之间的路程;两车相遇时S甲=S乙,解该一元一次方程即可求得两车相遇的时间.
(4)两车相遇300千米的情况有两种:相遇前和相遇后,故可列方程-180t+600-120t=300或120t-(-180t+600)=300,解方程求得t的值即可.
解:(1)![]()
![]() =120(千米/时);
=120(千米/时);
(2)S甲过点(3,60)和点(1,420),设S甲=kt+b,代入即可![]() ,解得
,解得![]() ,所以S甲与t的函数解析式为S甲=-180t+600;
,所以S甲与t的函数解析式为S甲=-180t+600;
设S乙=mt,将点(1,120)代入解析式可得:m=120,
S乙与t的函数解析式为s乙=120t;
(3)当t=0时,S甲的值表示两城之间的路程,此时S甲=600,故两城之间的路程为600千米;两车相遇时两车相遇时S甲=S乙,即-180t+600=120t,解得t=2.
(4)当相遇前两车相距300千米时,S甲-S乙=300,即-180t+600-120t=300,解得t=1;
当相遇后两车相距300千米时,S乙-S甲=300,即120t+180t-600=300,解得t=3.
当两车相距300千米时,t的值为1或3.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象
)的图象![]() 经过点
经过点![]() (4,1),直线
(4,1),直线![]() 与图象
与图象![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有4个整点,结合函数图象,求
内恰有4个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]
(1)求该抛物线的解析式;
(2)试求线段![]() 的长
的长![]() 关于点
关于点![]() 的横坐标
的横坐标![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
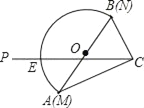
【题目】如图是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN重合,其量角器最外缘的读数是从N点开始(即N点的读数为0),现有射线CP绕着点C从CA顺时针以每秒2度的速度旋转到与△ACB外接圆相切为止.在旋转过程中,射线CP与量角器的半圆弧交于E.
(1)当射线CP与△ABC的外接圆相切时,求射线CP旋转度数是多少?
(2)当射线CP分别经过△ABC的外心、内心时,点E处的读数分别是多少?
(3)当旋转7.5秒时,连接BE,求证:BE=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2
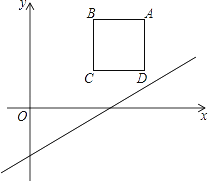
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学综合实践课上,老师提出问题:如图,有一张长为4dm,宽为3dm的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究: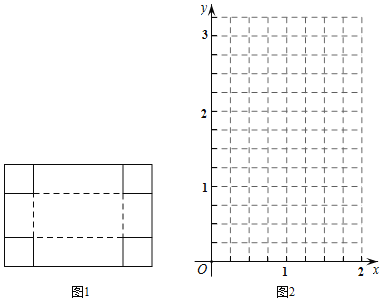
(1)设小正方形的边长为xdm,长方体体积为ydm3,根据长方体的体积公式,可以得到y与x的函数关系式是 ,其中自变量x的取值范围是 .
(2)列出y与x的几组对应值如下表:
x/dm | … |
|
|
|
|
|
|
| 1 |
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
(注:补全表格,保留1位小数点)
(3)如图,请在平面直角坐标系中描出以补全后表格中各对对应值为坐标的点,画出该函数图象;
(4)结合函数图象回答:当小正方形的边长约为 dm时,无盖长方体盒子的体积最大,最大值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.

(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1000元人民币购进某种水果销售,过了一周时间,又用2400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于1240元,则每千克这种水果的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com