

| 种类 | A | B | C | D |
| 变化 | 有利于延缓社会老龄化现象 | 导致人口暴增 | 提升家庭抗风险能力 | 增大社会基本公共服务的压力 |
分析 (1)根据统计图中的数据可以求得参与调查的市民一共有多少人;
(2)根据统计图可以得到选择C的人数;
(3)根据数学统计图可以得到∠α的度数;
(4)根据统计图中的数据可以得到选B和C的人数,从而可以将条形统计图补充完整.
解答 解:(1)80÷40%=200,
故答案为:200;
(2)参与调查的市民中选择C的人数是:200-80-(200×20%)-30=50,
故答案为:50;
(3)360°×20%=72°,
故答案为:72°;
(4)选择B的人数为:200×20%=40,
选择C的人数为:50,
故补全的条形统计图如右图所示,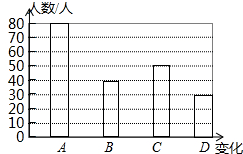
点评 本题考查条形统计图、扇形统计图、统计表,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com