
 在△ABC中,∠A=120°,AB=12,AC=6.求tanB的值.
在△ABC中,∠A=120°,AB=12,AC=6.求tanB的值. 分析 过点C作CD⊥AB,根据∠A=120°,∠DAC=60°,由三角函数得出AD,CD,在Rt△BCD中,∠B的正切即可得出答案.
解答 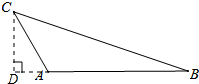 解:过点C作CD⊥AB,交BA的延长线于点D,
解:过点C作CD⊥AB,交BA的延长线于点D,
∴∠A=120°,
∴∠DAC=60°,
∴cos60°=$\frac{AD}{AC}$,sin60°=$\frac{CD}{AC}$,
∵AB=12,AC=6,
∴AD=AC•cos60°=6×$\frac{1}{2}$=3,
CD=AC•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
在Rt△BCD中,tanB=$\frac{CD}{BD}$=$\frac{3\sqrt{3}}{15}$=$\frac{\sqrt{3}}{5}$.
点评 本题考查了解直角三角形,解直角三角形的关键是把给出的这些三角形的条件放到直角三角形中,如果不是直角三角形就要通过添加辅助线来完成.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | $\frac{1}{9}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
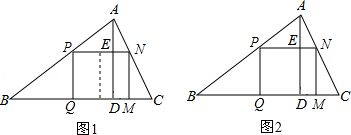
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $m<\frac{1}{4}$ | B. | $m<-\frac{1}{4}且m≠-2$ | C. | $m<-\frac{1}{4}$ | D. | $m<\frac{1}{4}且m≠-2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com