
【题目】在![]() 中,斜边AC的中点M关于BC的对称点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.
中,斜边AC的中点M关于BC的对称点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.
(1)在①![]() ,②
,②![]() ,③
,③![]() 中,等于旋转角的是 (填出满足条件的角的序号);
中,等于旋转角的是 (填出满足条件的角的序号);
(2)若![]() 求
求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)点N是BD的中点,连接MN,用等式表示线段MN与BE之间的数量关系,并证明.

【答案】(1)③;(2) ![]() ;(3)
;(3)![]() .证明见解析.
.证明见解析.
【解析】试题分析:(1)根据旋转角的定义判断即可;
(2)连接![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由直角三角形斜边上的中线等于斜边的一半,得
,由直角三角形斜边上的中线等于斜边的一半,得![]() ,由等边对等角得
,由等边对等角得![]() ,再由三角形外角的性质得
,再由三角形外角的性质得![]() ,由轴对称性质得
,由轴对称性质得![]() ,由同弧所对的圆周角是圆心角的一半可证得
,由同弧所对的圆周角是圆心角的一半可证得![]() ;
;
(3)连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,连接
,连接![]() .可证得四边形
.可证得四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,由三角形的中位线等于底边的一半,可证.
,由三角形的中位线等于底边的一半,可证.
(1)③;
(2)连接![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,

∵![]() 中,
中, ![]() °,
°,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() =
= ![]() ,
,
∴![]() ,
,
∵点M和点O关于直线BC对称,
∴![]() .
.
∵![]() ,
,
∴点C,B,E在以O为圆心, ![]() 为半径的圆上,
为半径的圆上,
∴![]() ;
;
(3)![]() .证明如下:
.证明如下:
连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,连接
,连接![]() .
.

∵![]() °,
°,
∴![]() °-
°-![]() °
°![]() ,
,
∴![]()
![]() °
°![]() ,
,
∵![]() ,
,
∴![]() °,
°,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() °
°![]() ,
,
∴![]() °,
°,
∴![]() °,
°,
∴![]() ∥
∥![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.
(1)求y关于x的函数解析式;
(2)若该种商品每千克的成本为30元,当每千克的销售价为多少元时,获得的利润为600元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+2S2+2S3+S4=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计一个鱼塘里鱼的数量,第一次打捞上来20条,做上记号放入水中,第二次打捞上来25条,其中4条有记号,鱼塘大约有鱼__________条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 P ( m + 3 , m + 1 )在 x 轴上,则 P 点坐标为( )
A.( 0 ,﹣ 2 )B.( 0 ,﹣ 4 )C.( 4 , 0 )D.( 2 , 0 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( )
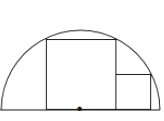
A. (4+![]() )cm B. 9cm C. 4
)cm B. 9cm C. 4![]() cm D. 6
cm D. 6![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )
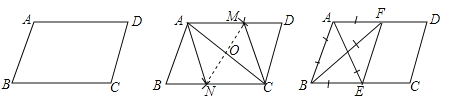
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
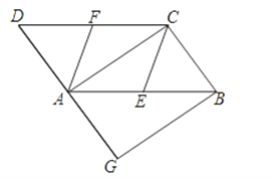
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com