
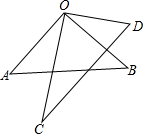
 如图,∠AOB=∠COD=90°,
如图,∠AOB=∠COD=90°,分析 (1)通过计算,寻找和为180°的两个角;
(2)由于∠AOD与∠COB互补,把∠COB=$\frac{3}{7}$∠AOD代入求出∠AOD.
解答  解:(1)互为补角的角有:∠AOD与∠COB,∠AOB与∠COD
解:(1)互为补角的角有:∠AOD与∠COB,∠AOB与∠COD
理由:∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°;
∴∠AOC=∠BOD,
∵∠AOB+∠COD=180°,
∠COD=∠COB+∠BOD
∴∠AOB+∠BOD+∠COB=180°,
即∠AOD+∠COB=180°.
(2)∵∠COB=$\frac{3}{7}$∠AOD,
又∵∠AOD+∠COB=180°,
∴$\frac{10}{7}$∠AOD=180°,
∴∠AOD=126°.
∠AOD的度数为126°.
点评 本题考查了互补、角的和差的计算等知识.利用互补关系及角间关系,通过方程的思想是解决本题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:解答题
 如图,G为BC的中点,且DG⊥BC,DE⊥AB于E,DF⊥AC于F,BE=CF.
如图,G为BC的中点,且DG⊥BC,DE⊥AB于E,DF⊥AC于F,BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
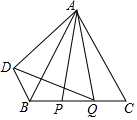 如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点B、C同时出发,运动速度均为2cm/s.点P从B点出发,沿B→C运动,到点C停止,点Q从点C出发,沿C→B运动,到点B停止,连接AP、AQ,点P关于直线AB的对称点为D,连接BD、DQ,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
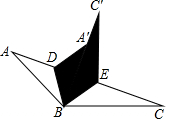 如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.
如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
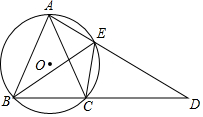 如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O交于点E,连接BE,CE.
如图,△ABC内接于⊙O,且AB=AC,延长BC至点D,使CD=AC,连接AD交⊙O交于点E,连接BE,CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx与x轴交于点A(4,0),点B(1,3)在抛物线上,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
如图,抛物线y=ax2+bx与x轴交于点A(4,0),点B(1,3)在抛物线上,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com