
 如图,将△ABC的边AB延长2倍至点A1,边BC延长2倍至点B1,边CA延长2倍至点C1,顺次连结A1、B1、C1,得△A1B1C1,再分别延长△A1B1C1的各边2倍得△A2B2C2,…,依次这样下去,得△AnBnCn,若△ABC的面积为1,则△AnBnCn的面积为19n.
如图,将△ABC的边AB延长2倍至点A1,边BC延长2倍至点B1,边CA延长2倍至点C1,顺次连结A1、B1、C1,得△A1B1C1,再分别延长△A1B1C1的各边2倍得△A2B2C2,…,依次这样下去,得△AnBnCn,若△ABC的面积为1,则△AnBnCn的面积为19n. 分析 根据等底的三角形高的比等于面积比推理出△A1B1C的面积是△A1BC面积的2倍,则△A1B1B的面积是△A1BC面积的3倍…,以此类推,得出△A2B2C2的面积.
解答 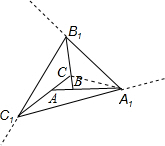 解:连接A1C,根据A1B=2AB,得到:AB:A1A=1:3,
解:连接A1C,根据A1B=2AB,得到:AB:A1A=1:3,
因而若过点B,A1作△ABC与△AA1C的AC边上的高,则高线的比是1:3,
因而面积的比是1:3,则△A1BC的面积是△ABC的面积的2倍,
设△ABC的面积是a,则△A1BC的面积是2a,
同理可以得到△A1B1C的面积是△A1BC面积的2倍,是4a,
则△A1B1B的面积是6a,
同理△B1C1C和△A1C1A的面积都是6a,
△A1B1C1的面积是19a,
即△A1B1C1的面积是△ABC的面积的19倍,
同理△A2B2C2的面积是△A1B1C1的面积的19倍,
即△A1B1C1的面积是19,△A2B2C2的面积192,
依此类推,△AnBnCn的面积是Sn=19n.
故答案为:19n.
点评 考查了三角形的面积,正确判断相邻的两个三角形面积之间的关系是解决本题的关键,本题的难度较大.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
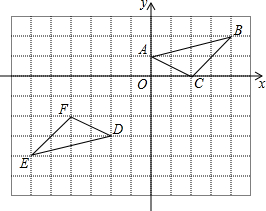 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心P点的坐标为(-1,-1).
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心P点的坐标为(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
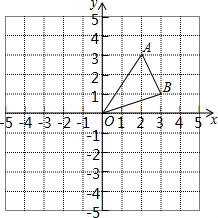 在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.
在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com