
分析 (1)根据实数的运算方法,首先计算开方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
(2)首先根据解一元一次不等式组的方法,求出不等式组的解集是多少;然后根据不等式组的解集,判断出它的所有整数解即可.
解答 解:(1)|2-$\sqrt{2}$|+$\frac{1}{2}$$\sqrt{(-2)^{2}}$+$\sqrt{2}$+$\frac{1}{\sqrt{2}}$+$\sqrt{2}$
=2-$\sqrt{2}$$+\frac{1}{2}×2+\sqrt{2}+\frac{\sqrt{2}}{2}+\sqrt{2}$
=2-$\sqrt{2}+1$$+\sqrt{2}+\frac{\sqrt{2}}{2}+\sqrt{2}$
=3$+\frac{3\sqrt{2}}{2}$
(2)∵$\left\{\begin{array}{l}{3x+1<x-3}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1}\end{array}\right.$
∴$\left\{\begin{array}{l}{x<-2}\\{x≥-5}\end{array}\right.$,
∴不等式组的解集是:-5≤x<-2,
∴它的所有整数解是:-5、-4、-3.
点评 (1)此题主要考查了实数的四则混合运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了解一元一次不等式组的方法,以及一元一次不等式组的整数解的判断,要熟练掌握.


科目:初中数学 来源: 题型:解答题
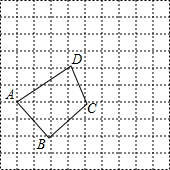 如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上.
如图,网格中的每一格的边长为1个单位长度,已知四边形ABCD的顶点均在网格的个点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$
(1)计算:|1-$\sqrt{2}$|+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{1}{4}}$-$\sqrt{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一扇正门和两扇侧门,1分钟内可以通过280名学生;当同时开启一扇正门和一扇侧门时,4分钟内可通过800名学生.
某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一扇正门和两扇侧门,1分钟内可以通过280名学生;当同时开启一扇正门和一扇侧门时,4分钟内可通过800名学生.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
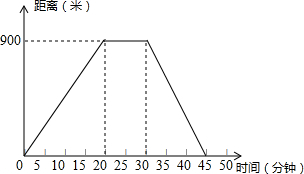 阳阳离开家去新华书店买书,回来后,阳阳用所学知识绘制了一张反映他离家的距离与时间的关系图,请根据阳阳绘制的这张图回答以下问题:
阳阳离开家去新华书店买书,回来后,阳阳用所学知识绘制了一张反映他离家的距离与时间的关系图,请根据阳阳绘制的这张图回答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 星期天早上,小明在锻炼身体,先从家跑步到公园,接着马上原路步行回家;如图是反映小明离家的路程y(米)与时间t(分)之间的函数关系的图象,则小明回家的速度是每分钟步行80米.
星期天早上,小明在锻炼身体,先从家跑步到公园,接着马上原路步行回家;如图是反映小明离家的路程y(米)与时间t(分)之间的函数关系的图象,则小明回家的速度是每分钟步行80米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com