分析 （1）先由直线y=x-4与x轴、y轴分别交于点A、B两点，求出点A、B的坐标，然后将其代入抛物线的解析式，得到关于b，c的方程组，求出b，c的值可得抛物线的解析式，再令y=0，求出x的值可得点C的坐标；
（2）首先根据平移条件表示出移动后的函数解析式，进而用m表示出该函数的顶点坐标，将其代入直线BC、AB的解析式中，即可确定P在△ABC内时m的取值范围；
（3）分两种情况：点M在点A的下方和点M在点A的上方，过点M作y轴的垂线，得到与△OCB相似的三角形，利用相似三角形对应边的比相等的性质进行求解即可．
解答 解：（1）∵直线y=x-4与x轴、y轴分别交于点A、B两点，
∴A（4，0）、B（0，-4），
∵抛物线y=$\frac{1}{3}$x2+bx+c经过A、B两点，
∴$\left\{\begin{array}{l}{\frac{16}{3}+4b+c=0}\\{c=-4}\end{array}\right.$，解得$\left\{\begin{array}{l}{b=-\frac{1}{3}}\\{c=-4}\end{array}\right.$，
∴抛物线的解析式为y=$\frac{1}{3}$x2-$\frac{1}{3}$x-4，
令y=0，得$\frac{1}{3}$x2-$\frac{1}{3}$x-4=0，解得x1=-3，x2=4，
∴点C的坐标为（-3，0）；
（2）∵m＜0，
∴|m|=-m，
∵y=$\frac{1}{3}$x2-$\frac{1}{3}$x-4=$\frac{1}{3}$（x-$\frac{1}{2}$）2-$4\frac{1}{12}$
由题意，新抛物线的解析式可表示为：y=$\frac{1}{3}$（x-$\frac{1}{2}$+m）2-$4\frac{1}{12}$+$3\frac{1}{12}$=$\frac{1}{3}$（x-$\frac{1}{2}$+m）2-1，
它的顶点坐标P（$\frac{1}{2}$-m，-1）；
设直线BC的解析式为y=kx+n（k≠0），把点B、C的坐标代入得$\left\{\begin{array}{l}{-3k+n=0}\\{n=-4}\end{array}\right.$，
∴k=$-\frac{4}{3}$，n=-4，
∴直线BC的解析式为y=$-\frac{4}{3}$x-4，
当点P在直线BC上时，$-\frac{4}{3}$（$\frac{1}{2}$-m）-4=-1，解得m=$\frac{11}{4}$，
当点P在直线AB上时，$\frac{1}{2}$-m-4=-1，解得m=$-\frac{5}{2}$，
∴当点P在△ABC内时，$-\frac{5}{2}$＜m＜$\frac{11}{4}$，
又∵m＜0，
∴$-\frac{5}{2}$＜m＜0；
（3）∵点A（4，0）、B（0，-4），
∴△AOB是等腰直角三角形，∠OBA=90°，
当点M在点A的下方时，如图1，作MN⊥y轴与N，则∠MNB=90°，
设点M的坐标为（a，$\frac{1}{3}$a2-$\frac{1}{3}$a-4），则MN=a，ON=-$\frac{1}{3}$a2+$\frac{1}{3}$a+4，BN=$\frac{1}{3}$a2-$\frac{1}{3}$a，
∵∠MBA+∠CBO=45°，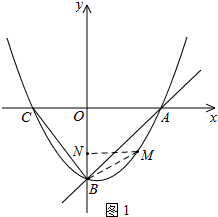
∴∠CBM=90°=∠OBC+∠NBM，
又∵∠OCB+∠OBC=90°，
∴∠OCB=∠NBM，
又∵∠COB=∠BNM=90°，
∴△OCB∽△NBM，
∴OC：OB=NB：NM，即3：4=（$\frac{1}{3}$a2-$\frac{1}{3}$a）：a，
解得a=$\frac{13}{4}$，
∴点M的坐标为$（\frac{13}{4}，-\frac{25}{16}）$；
当点M在点A的上方时，如图2，作MH⊥y轴与H，则∠MHB=90°，
∵设点M的坐标为（e，$\frac{1}{3}$e2-$\frac{1}{3}$e-4），则MH=e，BH=$\frac{1}{3}$e2-$\frac{1}{3}$e，
∵∠MBA+∠CBO=45°，∠OBA=45°，
∴∠OBC=∠HBM，
又∵∠COB=∠MHB，
∴△OBC∽△HBM，
∴OC：OB=HM：HB，即3：4=e：（$\frac{1}{3}$e2-$\frac{1}{3}$e），
解得e=5，
∴点M的坐标为（5，$\frac{8}{3}$），
综上所述，点M的坐标为$（\frac{13}{4}，-\frac{25}{16}）$或（5，$\frac{8}{3}$）．
点评 本题考查了二次函数综合应用，相似三角形的判定与性质，待定系数法求一次函数的解析式，坐标与图形性质等知识，具有一定的综合性，难度较大，解答问题（3）时注意分类讨论，通过构建相似三角形是解题的关键，同时注意数形结合思想的运用．
科目：初中数学 来源： 题型：选择题
| A． | 全等三角形的对应边相等，对应角相等 | |
| B． | 全等三角形的对应边上的中线相等 | |
| C． | 两条边和一个角对应相等的两个三角形全等 | |
| D． | 全等三角形的面积相等 |
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
如图，点B、E、F、C在一条直线上，AB=DE=10，AC=DF，BE=CF=CE．