【题目】如图，在Rt△ABC中，∠BAC=90°，AB=3，M为边BC上的点，连接AM．如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是_____．
【答案】2
【解析】
如图，作ME⊥AC于E，MF⊥AB于F，点D为AC的中点，根据折叠的性质得AD=AB=3，∠BAM=∠CAM，则AC=2AD=6，根据角平分线定理得ME=MF，然后利用面积法得到
MFAB+MEAC=ABAC，即3ME+6ME=3×6，解得ME=2．
如图,
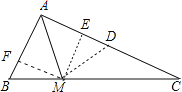
作ME⊥AC于E，MF⊥AB于F，点D为AC的中点，
∵△ABM沿直线AM翻折后，点B恰好落在边AC的中点D处，
∴AD=AB=3,∠BAM=∠CAM=45
，
∴AC=2AD=6，ME=MF，
∵S△ABM+S△AMC=S△ABC，
∴MF
AB+MEAC=ABAC，
∴3ME+6ME=3×6，
∴ME=2，
即点M到AC的距离是2.
故答案为2.
科目：初中数学 来源： 题型：
【题目】已知
与
是两个大小不同的等腰直角三角形．
如图①所示，连接
，
，试判断线段和的数量和位置关系，并说明理由；
如图②所示，连接，将线段绕
点顺时针旋转
到
，连接
，试判断线段
和的数量和位置关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：几个全等的正多边形依次有一边重合，排成一圈，中间可以围成一个正多边形，我们称作正多边形的环状连接。如图，我们可以看作正六边形的环状连接，中间围成一个边长相等的正六边形；若正八边形作环状连接，中间可以围的正多边形的边数为；
若正八边形作环状连接，中间可以围的正多边形的边数为________，若边长为1的正n边形作环状连接，中间围成的是等边三角形，则这个环状连接的外轮廓长为_________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知BC=EC，∠BCE=∠ACD，如果只添加一个条件，使△ABC ≌ △DEC，则添加的条件不能为（ ）
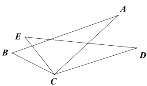
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】商场服装柜在销售中发现：某童装平均每天可售出
件，每件盈利
元．为了迎接“六一”国际儿童节，商场决定采取适当的降价措施，调查发现：如果每件童装降价
元，那么平均每天就可多售出
件．要想平均每天销售这种童装共盈利
元，设每件童装降价
元，那么应满足的方程是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察与探究：
(1)观察下列各组数据并填空：
A：1，2，3，4，5，
平均数xA＝________，方差sA2＝________；
B：11，12，13，14，15，
平均数xB＝________，方差sB2＝________；
C：10，20，30，40，50，
平均数xC＝________，方差sC2＝________；
(2)分别比较A与B，C的计算结果，你能发现什么规律？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表，得出下面结论：①抛物线与轴的一个交点为
；②函数的最大值为
；③抛物线的对称轴是
；④在对称轴左侧，随增大而增大．其中正确有（ ）
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
