
【题目】已知数轴上有![]() 两点,分别表示的数为
两点,分别表示的数为![]() 和
和![]() ,且
,且![]() ,点
,点![]() 以每秒3个单位长度的速度沿数轴向左匀速运动,点
以每秒3个单位长度的速度沿数轴向左匀速运动,点![]() 以每秒2个单位长度的速度向右匀速运动.设运动时间为
以每秒2个单位长度的速度向右匀速运动.设运动时间为![]() 秒(
秒(![]() ).
).
(1)![]() ______,
______,![]() ______;
______;
(2)运动开始前,![]() 两点之间的距离为________;
两点之间的距离为________;
(3)它们按上述方式运动,![]() 两点经过多少秒会相遇?相遇点所表示的数是什么?
两点经过多少秒会相遇?相遇点所表示的数是什么?
(4)当![]() 为多少秒时,
为多少秒时,![]() 两点之间的距离为2?请直接写出结果.
两点之间的距离为2?请直接写出结果.
【答案】(1)12;38(2)50(3)10秒,相遇点所表示的数是18.(4)t为![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)利用绝对值的非负性,可求出a,b值;
(2)由点A,B表示的数可求出线段AB的长;
(3)当运动时间为t秒时,点A表示的数为3t+12,点B表示的数为2t38,由A,B两点相遇,可得出关于t的一元一次方程,解之即可得出结论;
(4)根据线段AB=2,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论.
(1)∵|a12|+|b+38|=0,
∴a12=0,b+38=0,
∴a=12,b=38.
故答案为:12;38.
(2)AB=12(38)=50.
故答案为:50.
(3)当运动时间为t秒时,点A表示的数为3t+12,点B表示的数为2t38,
依题意,得:3t+12=2t38,
解得:t=10.
∴3t+12=18.
答:A,B两点经过10秒会相遇,相遇点所表示的数是18.
(4)依题意,得:|3t+12(2t38)|=2,
即505t=2或5t50=2,
解得:t=![]() 或t=
或t=![]() .
.
答:当t为![]() 秒或
秒或![]() 秒时,A,B两点之间的距离为2.
秒时,A,B两点之间的距离为2.


科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中有一个黑球![]() 和两个白球
和两个白球![]() (除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球,则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的数学兴趣小组在活动中,对“线段中点”问题进行以下探究.已知线段![]() ,点
,点![]() 为
为![]() 上一个动点,点
上一个动点,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(1)如图1,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,求
,求![]() 的长度;
的长度;
(2)如图2,若点![]() 是线段
是线段![]() 上任意一点,则
上任意一点,则![]() 的长度为______
的长度为______![]() ;
;
(3)若点![]() 在线段
在线段![]() 的延长线上,其余条件不变,借助图3探究
的延长线上,其余条件不变,借助图3探究![]() 的长度,请直接写出
的长度,请直接写出![]() 的长度(不写探究过程).
的长度(不写探究过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
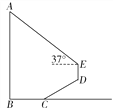
【题目】(题文)如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方2![]() m处的点C出发,沿斜面坡度i=1∶
m处的点C出发,沿斜面坡度i=1∶![]() 的斜坡CD前进4m到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5 m.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4m到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5 m.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,计算结果保留根号)
,计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距480km路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1h,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车调头的时间忽略不计),快、慢两车距乙地的路程ykm与所用时间xh之间的函数图像如图所示,请结合图像信息解答下列问题:
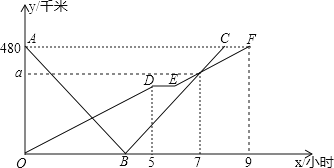
(1)直接写出慢车的行驶速度和a的值;
(2)求快车的速度和B点坐标;
(3)快车和慢车第一次相遇时,距离甲地的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
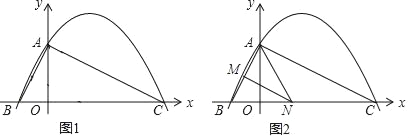
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com