练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．
    （1）求证：△ABD是等腰三角形．
    （2）若AB=AC=12，△CBD的周长为20，求线段BC的长．
    考点：线段垂直平分线的性质,等腰三角形的判定与性质
    专题：
    分析：（1）根据线段垂直平分线得出AD=BD，即可得出答案；
    （2）根据△BCD周长得出BC+AC=20，代入即可求出答案．
    解答：（1）证明：∵AB的垂直平分线DE，
    ∴AD=BD，
    ∴△ABD是等腰三角形；

    （2）解：∵△CBD的周长为20，
    ∴BC+CD+BD=BC+CD+AD=BC+AC=20，
    ∵AC=12，
    ∴BC=8．
    点评：本题考查了线段垂直平分线和等腰三角形性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，点P是∠AOB的边OB上一点，读句画图，并回答问题
    （1）过P画OA的垂线，垂足为H；过点P画OB的垂线，交OA于点C．
    ①其中线段
     
     的长表示点P到OA的距离．
    ②比较PH与PC的大小得PH
     
     PC．（用“＞”，“=”，“＜”填空）
    （2）过点P画OA的平行线PD．度量∠AOB与∠DPB的大小得∠AOB
     
    ∠DPB．（用“＞”，“=”，“＜”填空）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    求一个正数的算术平方根，有些数可以直接可得，如
    		4
    ；有些数则不能直接求得，如
    		5
    ，除通过计算器可以求得．还可以通过一组数的内在联系，运用规律求得，观察下表：
    n 0.09 9 900 90000 …
    		n
    		 0.3 3 30 300 …
    （1）根据表中的规律，可以求得：
    		0.0009
    =
     
    ，
    		9000000
    =
     
    ；
    （2）根据表中的规律，还可以由
    		2.06
    =1.435    ，求得：
    		0.0206
    =
     
    ，
    		20600
    =
     
    ，
    		8.24
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    化简：
    （1）-m2-n2-（-2mn-m2+n2）
    （2）5（x2-3）-2（3x2+5 ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，∠A=90°，∠C的平分线交AB于D，若∠DCB=2∠B，求∠ADC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简，再求值：（3a2-ab+7）-（5ab-4a2+7）．其中a=
    1
    3
    ．B=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

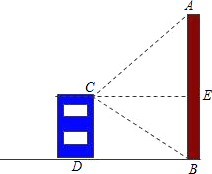    在旧城改造中，要拆除一烟囱AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在从离B点21米远的建筑物CD顶端C测得A点的仰角为45°，到B点的俯角为30°，问离B点30米远的保护文物是否在危险区内？（
    		3
    约等于1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）3
    		3
    +
    		2
    -2
    		2
    -2
    		3
    ；
    （2）
    		24
    ÷
    		3
    -
    1
    2
    ×
    		18
    +
    		32
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    有理数a，b在数轴上对应点如图所示，则
    a-b
    ab
    ＜0，若|a|=1，|b|=2.5，则|a+b|的值是
     
    ．

    查看答案和解析>>

    同步练习册答案