
【题目】如图,在△ABC中,AB=2,AC= ![]() ,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 . 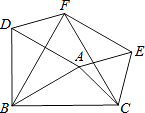
【答案】2
【解析】解:∵△ABD,△ACE都是等边三角形, ∴∠DAB=∠EAC=60°,
∵∠BAC=105°,
∴∠DAE=135°,
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,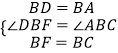
∴△ABC≌△DBF(SAS),
∴AC=DF=AE= ![]() ,
,
同理可证△ABC≌△EFC,
∴AB=EF=AD=2,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°﹣∠DAE=45°,
∴SAEFD=AD(DFsin45°)=2×( ![]() ×
× ![]() )=2.
)=2.
即四边形AEFD的面积是2,
所以答案是:2.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
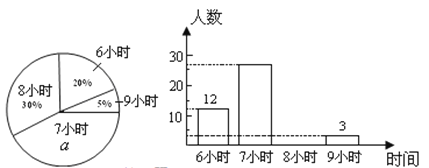
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形. 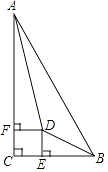
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )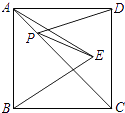
A.![]()
B.3
C.4
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙、丙、丁共有30本,又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为2:3:4:1,则乙的课外书的本数为( )
A.6本
B.9本
C.11本
D.12本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,∠B=25°,AB=5,则BC的长为( )
A.5sin25°B.5tan65°C.5cos25°D.5tan25°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com