
【题目】如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )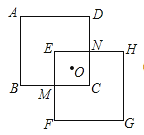
A.M或O或N
B.E或O或C
C.E或O或N
D.M或O或C
【答案】A
【解析】若以M为旋转中心,把正方形ABCD顺时针旋转90°,A点对应点为H,B点对应点为E,C点对应点为F,D点对应点为G,则可得到正方形EFGH;
若以O为旋转中心,把正方形ABCD旋转180°,A点对应点为G,B点对应点为H,C点对应点为E,D点对应点为F,则可得到正方形EFGH;
若以N为旋转中心,把正方形ABCD逆时针旋转90°,A点对应点为F,B点对应点为G,C点对应点为H,D点对应点为E,则可得到正方形EFGH.
故选A.
分类:若以M为旋转中心,把正方形ABCD顺时针旋转90°;若以O为旋转中心,把正方形ABCD旋转180°;若以N为旋转中心,把正方形ABCD逆时针旋转90°,然后通过分别找出正方形EFGH与正方形ABCD的对应点来判断正方形EFGH是否由正方形ABCD绕某点旋转得到.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,两个反比例函数C1:y=![]() 和C2:y=
和C2:y=![]() 在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1- k2;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点
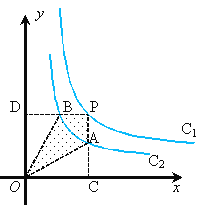
A. ①② B. ②④ C. ①②④ D. ①③④
【答案】C
【解析】①∵A、B两点都在y=![]() 上,∴△ODB与△OCA的面积都都等于
上,∴△ODB与△OCA的面积都都等于![]() ,则①正确;②S矩形OCPB-S△AOC-S△DBO=|k2|-2×|k1|÷2=k2-k1,则②正确;③只有当P的横纵坐标相等时,PA=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选C.
,则①正确;②S矩形OCPB-S△AOC-S△DBO=|k2|-2×|k1|÷2=k2-k1,则②正确;③只有当P的横纵坐标相等时,PA=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选C.
【题型】单选题
【结束】
10
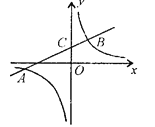
【题目】如图,反比例函数![]() (k>0)与一次函数
(k>0)与一次函数![]() 的图象相交于两点A(
的图象相交于两点A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),线段AB交y轴与C,当|
),线段AB交y轴与C,当|![]() -
-![]() |=2且AC = 2BC时,k、b的值分别为( )
|=2且AC = 2BC时,k、b的值分别为( )
A. k=![]() ,b=2 B. k=
,b=2 B. k=![]() ,b=1 C. k=
,b=1 C. k=![]() ,b=
,b=![]() D. k=
D. k=![]() ,b=
,b=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形(长方形),点A、C的坐标分别为A(10,0 ),C(0,4),点D是OA的中点,点P在线段BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 ____________________________________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是(写出正确结论的序号)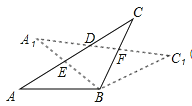
查看答案和解析>>
科目:初中数学 来源: 题型:
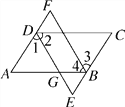
【题目】(南阳唐河县期中)如图,在ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC. 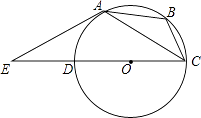
(1)求∠B的度数;
(2)若ED=1,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com