【题目】综合题。
（1）已知 
，用含a,b的式子表示下列代数式。
①求: 
的值 ②求: 
的值
（2）已知 
,求x的值.
【答案】
（1）
解：∵ 4m= a , 8n= b ，
∴ 22m= a , 23n= b.
①22m+3n=22m×23n＝ab.
② 24m-6n=24m÷26n=(22m)2÷(23n)2=a2÷b2=
.
（2）
解： 2×8x×16 = 223 ,
2×23x×24=223,
21+3x+4=223,
即1+3x+4=23，
解得x=6.
【解析】（1）由已知可得22m= a , 23n= b.运用了幂的乘方法则；
（2）运用同底数幂的乘法法则.
【考点精析】掌握同底数幂的乘法和同底数幂的除法是解答本题的根本，需要知道同底数幂的乘法法则aman=am+n(m,n都是正数)；同底数幂的除法法则：am÷an=am-n（a≠0，m，n都是正整数，且m＞n）．
科目：初中数学 来源： 题型：
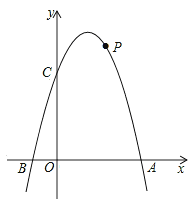
【题目】如图，已知二次函数y=﹣x2+bx+c的图象交x轴于点A（4，0）和点B，交y轴于点C（0，4）．
（1）求这个二次函数的表达式；
（2）若点P在第一象限内的抛物线上，求四边形AOCP面积的最大值和此时点P的坐标；
（3）在平面直角坐标系内，是否存在点Q，使A，B，C，Q四点构成平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了加快5G网络的建设，国家根据发展规划，自从2015年以来投入研发和建设的经费为164100000000元，将数164100000000用科学记数法表示为（ ）
A. 1.641×1012B. 0.1641×1013
C. 1.641×1011D. 1.641×1013
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程x2+px+q=0的两个根为x1=3，x2=﹣4，则二次三项式x2﹣px+q可分解为（ ）
A. （x+3）（x﹣4）B. （x﹣3）（x+4）C. （x+3）（x+4）D. （x﹣3）（x﹣4）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点O在线段AB上，AO＝2，OB＝1，OC为射线，且∠BOC＝60，动点P以每秒2个单位长度的速度从点O出发，沿射线OC做匀速运动，设运动时间为t秒．
（1）当t＝
时，则OP＝ ，S△ABP＝ ；
（2）当△ABP是直角三角形时，求t的值；
（3）如图2，当AP＝AB时，过点A作AQ∥BP，并使得∠QOP＝∠B，求证：AQ·BP＝3．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com