
| 销售量(万件) | 平均每件产品的利润(元) | |
| 网上销售 | x | 当0<x≤2时,y1=140 |
| 当2≤x<6时,y1=-5x+150 | ||
| 批发部销售 | n | 当0<n≤2时,y2=120 |
| 当2≤n<6时,y2=-5n+130 |
分析 (1)①将x=4.2代入y1=-5x+150,将n=6-4.2=1.8可得y2;
②由n=6-x,结合0<n≤2、2≤n<6可得对应x的范围及y2的表达式;
(2)分0<x≤2、2≤x≤4、4≤x<6三种情况,根据总利润=网上所获利润+批发部销售所获利润,结合表中不同范围内的单件利润的函数表达式即可得;
(3)由(2)中三种情况,根据二次函数的性质分别求出三个范围内的最大值,再比较即可得.
解答 解:(1)①当x=4.2时,n=6-4.2=1.8,
∴y1=-5×4.2+150=129,y2=120,
故答案为:129;120;
②∵x+n=6,
∴当0<n≤2时,即0<6-x≤2,解得,4≤x<6,此时y2=120,
∴当2≤n<6时,即2≤6-x<6,解得,0<x≤4,此时y2=-5(6-x)+130=5x+100,
故答案为:4,5x+100;4;
(2)由题意可得,
当0<x≤2时,w=140x+(5x+100)(6-x)=5x2+70x+600;
当2≤x≤4时,w=(-5x+150)x+(5x+100)(6-x)=-10x2+80x+600;
当4≤x<6时,w=(-5x+150)x+120(6-x)=-5x2+30x+720;
(3)当0<x≤2时,w=-5x2+70x+600=-5(x-7)2+845,
∵-5<0,且x<7时,w随x的增大而减小,
∴当x=2时,w最大=720;
当2≤x≤4时,w=-10x2+80x+600=-10(x-4)2+760,
∴当x=4时,w最大=760;
当4≤x<6时,w=-5x2+30x+720=-5(x-3)2+765,
∵-5<0,且x>3时,w随x的增大而减小,
∴当x=4时,w最大=760;
综上可知,该公司每年网上、批发部的销售量各为4万件、2万件时,可使公司每年的总利润最大,最大值为760万元.
点评 本题主要考查二次函数的应用,理解题意列出不同范围内单件利润的函数表达式是解题的根本,根据销售量x的不同范围分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
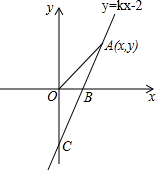 如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.
如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
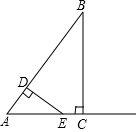 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
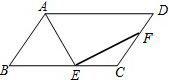 如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,EC=CF,若BC=7,DF=3,tan∠AEB=3,则平行四边形ABCD的面积为21.
如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,EC=CF,若BC=7,DF=3,tan∠AEB=3,则平行四边形ABCD的面积为21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若y-4=8,则y=8-4 | |
| B. | 若2(2x-3)=2,则4x-6=2 | |
| C. | 若-$\frac{1}{2}$x=4,则x=-2 | |
| D. | 若 $\frac{1}{3}$-$\frac{t-1}{2}$=1,则去分母得2-3(t-1)=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com