
【题目】(数学概念)
若等边三角形的三个顶点D、E、F分别在△ABC的三条边上,我们称等边三角形DEF是△ABC的内接正三角形.
(概念辨析)
(1)下列图中△DEF均为等边三角形,则满足△DEF是△ABC的内接正三角形的是 .
A.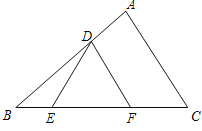 B.
B.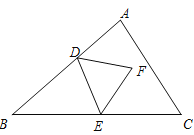
C.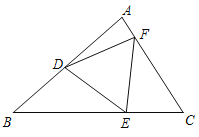
(操作验证)
(2)如图①.在△ABC中,∠B=60°,D为边AB上一定点(BC>BD),DE=DB,EM平分∠DEC,交边AC于点M,△DME的外接圆与边BC的另一个交点为N.
求证:△DMN是△ABC的内接正三角形.
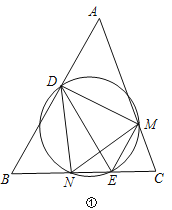
(知识应用)
(3)如图②.在△ABC中,∠B=60°,∠A=45°,BC=2,D是边AB上的动点,若边BC上存在一点E,使得以DE为边的等边三角形DEF是△ABC的内接正三角形.设△DEF的外接圆⊙O与边BC的另一个交点为K,则DK的最大值为 ,最小值为 .
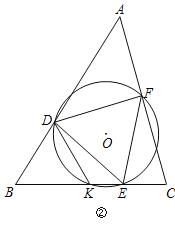
【答案】(1)C;(2)证明见解析;(3)2,![]() .
.
【解析】
(1)由概念即可得;
(2)由等弧所对的圆周角相等和角平分线定理即可证得;
(3)
(1)由概念即可得答案为:C;
(2)∵DE=DB,∠B=60°
∴∠DEB=∠B=60°
∴∠DMN=∠DEB=60°
∴∠DEC=180°-∠DEB=120°
∵EM平分∠DEC
∴∠DEM= ![]() ∠DEC=60°
∠DEC=60°
∴∠DNM=∠DEM==60°
∴∠NDM=180°-∠DMN-∠DNM=60°
∴∠NDM=∠DMN=∠DNM=60°
∴△DMN是正三角形
∵由概念得△DMN是△ABC的内接三角形
∴△DMN是△ABC的内接正三角形.
(3)2 ; ![]()
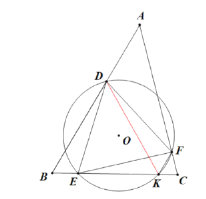
思路:①最大值
如图,当 K 与C 重合时, DK 最大,而△ BDK 是等边三角
形,所以 DK BK BC 2
②最小值
如右图,设 DK=BD=BK=x ,则CK=2- x .
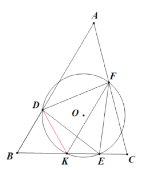
由手拉手模型:△ BDK 和△ DEF 都是等边三角形,且共点 D.易证△ BDE △ KDF .
∴ BE= KF
∵∠DKF=∠BDK= 60°,
∴ KF / / AB
∴![]()
即![]()
下面在图中求AB,
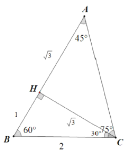
AB=![]() ,
,
![]()

∵BE≤BC=2,
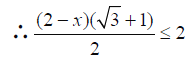


科目:初中数学 来源: 题型:
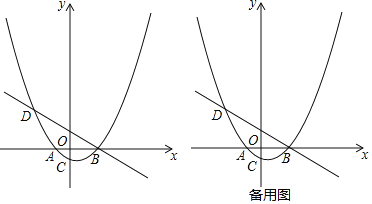
【题目】如图,已知抛物线y=a(x+2)(x-4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=-![]() x+b与抛物线的另一交点为D,且点D的横坐标为-5.
x+b与抛物线的另一交点为D,且点D的横坐标为-5.
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=8cm,BC=6cm,P点在BC上,从B点到C点运动(不包括 C点),点 P运动的速度为1cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2cm/s,若点 P、Q 分别从B、C 同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当 t 为何值时,P、Q 两点的距离为 4![]() cm?
cm?
(2)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
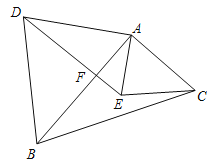
【题目】如图,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB与DE相交于点F,连接DB、CE.
(1)若![]() ,求∠AFD的度数;
,求∠AFD的度数;
(2)若∠ADE=∠ABC,求证△ADB∽△AEC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形 OABC 是矩形,点 B 的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线 m 从原点O出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 m 与矩形 OABC 的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若 MN=![]() AC,求 t 的值;
AC,求 t 的值;
②设△OMN 的面积为S,当 t 为何值时,S=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
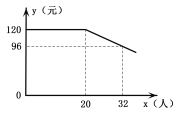
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com