
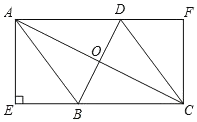
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=8,AD=10,求OE的长.
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]()
![]() 的图象与反比例函数
的图象与反比例函数![]()
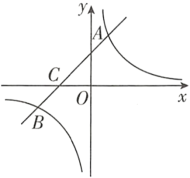
![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
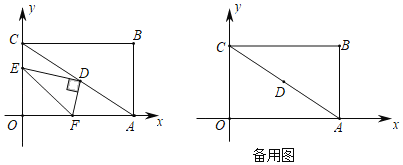
【题目】如图,在平面直角坐标系中,矩形OABC边OA,OC分别在x轴,y的正半轴上,且OA=8,OC=6,连接AC,点D为AC中点,点E从点C出发以每秒1个单位长度运动到点O停止,设运动时间为t秒(0<t<6),连接DE,作DF⊥DE交OA于点F,连接EF.
(1)当t的值为 时,四边形DEOF是矩形;
(2)用含t的代数式表示线段OF的长度,并说明理由;
(3)当△OEF面积为![]() 时,请直接写出直线DE的解析式.
时,请直接写出直线DE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
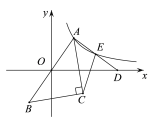
【题目】如图,点A与点B关于原点对称,点C在第四象限,∠ACB=90°.点D是![]() 轴正半轴上一点,AC平分∠BAD,E是AD的中点,反比例函数
轴正半轴上一点,AC平分∠BAD,E是AD的中点,反比例函数![]() (
(![]() )的图象经过点A,E.若△ACE的面积为6,则
)的图象经过点A,E.若△ACE的面积为6,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点A,B的坐标分别为(1,0),(0,2),AC⊥AB,且AB=AC,直线BC交![]() 轴于点D,抛物线
轴于点D,抛物线![]() 经过点A,B,D.
经过点A,B,D.

(1)求直线BC和抛物线![]() 的函数表达式;
的函数表达式;
(2)点P是直线BD下方的抛物线上一点,求△PCD面积的最大值,以及△PCD面积取得最大值时,点P的坐标;
(3)若点P的坐标为(2)小题中,△PCD的面积取得最大值时对应的坐标.平面内存在直线l,使点B,D,P到该直线的距离都相等,请直接写出所有满足条件的直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
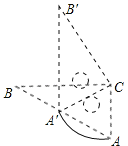
【题目】如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
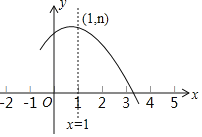
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:①4a﹣2b+c>0;②3a+b>0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个互异实根.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com