
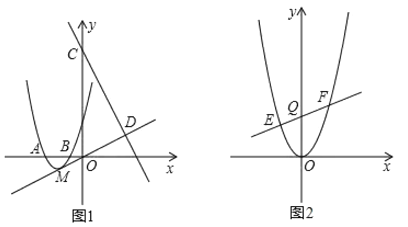
【题目】如图(1),抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图(2),将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为y=x2+4x+3;(2) h=4或![]() ≤h<
≤h<![]() ;(3)y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
;(3)y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
【解析】
(1)将A(-3,0)、B(-1,0),代入y=ax2+bx+3求出即可,再利用平方法求出顶点坐标即可;
(2)配方后即可确定其顶点坐标,然后利用平移规律确定函数的解析式,然后根据线段与抛物线有唯一的公共点求得h的值或取值范围即可;
(3)将抛物线平移,当顶点至原点时,其解析式为y=x2,设MN的解析式为y=kx+3(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过M,N作GH的垂线,垂足为G,H.根据△PMN的内心在y轴上,得到∠GMP=∠MPQ=∠QPN=∠HNP,从而△GMP∽△HNP,利用相似三角形对应边成比例即可列出有关t的方程求解即可.
(1)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点
∴9a-3b+3=0且a-b+3=0
解得a=1,b=4
∴抛物线的解析式为y=x2+4x+3
(2)由(1)配方得y=(x+2)2-1
∴抛物线的顶点M(-2,-1)
∴直线OM的解析式为y=![]() x
x
于是设平移的抛物线的顶点坐标为(h,![]() h),
h),
∴平移的抛物线解析式为y=(x-h)2+![]() h,.
h,.
①当抛物线经过点E时,
∵C(0,9),
∴h2+![]() h=9,
h=9,
解得h=![]() .
.
∴当![]() ≤h<
≤h<![]() 时,平移的抛物线与线段EF只有一个公共点.
时,平移的抛物线与线段EF只有一个公共点.
②当抛物线与线段CD只有一个公共点时,
由方程组y=(x-h)2+![]() h,y=-2x+9.
h,y=-2x+9.
得x2+(-2h+2)x+h2+![]() h-9=0,
h-9=0,
∴△=(-2h+2)2-4(h2+![]() h-9)=0,
h-9)=0,
解得h=4.
此时抛物线y=(x-4)2+2与线段CD唯一的公共点为(3,3),符合题意.
综上:平移的抛物线与线段CD只有一个公共点时,顶点横坐标的值或取值范围是h=4或![]() ≤h<
≤h<![]() .
.
(3)将抛物线平移,当顶点至原点时,其解析式为y=x2,
设EF的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.
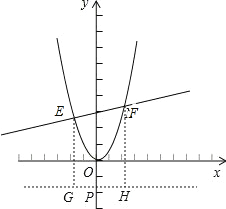
∵△PEF的内心在y轴上,
∴∠GEP=∠EPQ=∠QPF=∠HFP,
∴△GEP∽△HFP,
∴![]() ,
,
∴![]()
∴2kxExF=(t-3)(xE+xF)
由y=x2,y=kx+3.得x2-kx-3=0.
∴xE+xF=k,xExF=-3.
∴2k(-3)=(t-3)k,
∵k≠0,
∴t=-3.
∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.


科目:初中数学 来源: 题型:
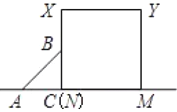
【题目】已知,如图等腰直角![]() 沿MN所在的直线以
沿MN所在的直线以![]() 的速度向右作匀速直线运动,若
的速度向右作匀速直线运动,若![]() ,则
,则![]() 和正方形
和正方形![]() 重叠部分的面积
重叠部分的面积![]() 与匀速运动所有的时间
与匀速运动所有的时间![]() 之间函数的大致图像是( )
之间函数的大致图像是( )
A.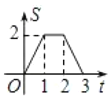 B.
B.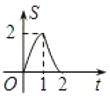 C.
C.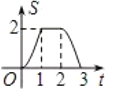 D.
D.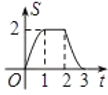
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018杭州马拉松竞赛”的个人竞赛项目共有三项:A.“马拉松”,B.“半程马拉松”,C.“迷你马拉松”.小明和小刚参加了该赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为![]() ______.
______.
(2)请用画树状图或列表的方法,求出小明和小刚被分配到同一项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
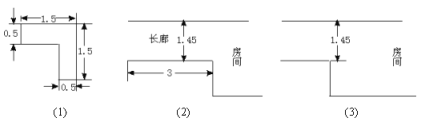
【题目】如图(1)所示是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2米,房间高2.6米,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图(2)中的长廊搬入房间.在图(3)中把你设计的方案画成草图,并说明按此方案可把家具搬入房间的理由(注:搬运过程中不准拆卸家具,不准损坏墙壁).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】修建隧道可以方便出行.如图:![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要爬坡到山顶
地需要爬坡到山顶![]() 地,再下坡到
地,再下坡到![]() 地.若打通穿山隧道,建成直达
地.若打通穿山隧道,建成直达![]() ,
,![]() 两地的公路,可以缩短从
两地的公路,可以缩短从![]() 地到
地到![]() 地的路程.已知:从
地的路程.已知:从![]() 到
到![]() 坡面的坡度
坡面的坡度![]() ,从
,从![]() 到
到![]() 坡面的坡角
坡面的坡角![]() ,
,![]() 公里.
公里.
(1)求隧道打通后从![]() 到
到![]() 的总路程是多少公里?(结果保留根号)
的总路程是多少公里?(结果保留根号)
(2)求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程约缩短多少公里?(结果精确到0.01)(
地的路程约缩短多少公里?(结果精确到0.01)(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段路的“拥堵延时指数”计算公式为:拥堵延时指数=![]() ,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的
,指数越大,道路越堵。高德大数据显示第二季度重庆拥堵延时指数首次排全国榜首。为此,交管部门在A、B两拥堵路段进行调研:A路段平峰时汽车通行平均时速为45千米/时,B路段平峰时汽车通行平均时速为50千米/时,平峰时A路段通行时间是B路段通行时间的![]() 倍,且A路段比B路段长1千米.
倍,且A路段比B路段长1千米.
(1)分别求平峰时A、B两路段的通行时间;
(2)第二季度大数据显示:在高峰时,A路段的拥堵延时指数为2,每分钟有150辆汽车进入该路段;B路段的拥堵延时指数为1.8,每分钟有125辆汽车进入该路段。第三季度,交管部门采用了智能红绿灯和潮汐车道的方式整治,拥堵状况有明显改善,在高峰时,A路段拥堵延时指数下降了a%,每分钟进入该路段的车辆增加了![]() ;B路段拥堵延时指数下降
;B路段拥堵延时指数下降![]() ,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多
,每分钟进入该路段的车辆增加了a辆。这样,整治后每分钟分别进入两路段的车辆通过这两路段所用时间总和,比整治前每分钟分别进入这两段路的车辆通过这两路段所用时间总和多![]() 小时,求a的值.
小时,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com