
如图,二次函数 的图象与x轴交于两个不同的点A(﹣2,0)、B(4,0),与y轴交于点C(0,3),连接BC、AC,该二次函数图象的对称轴与x轴相交于点D.
的图象与x轴交于两个不同的点A(﹣2,0)、B(4,0),与y轴交于点C(0,3),连接BC、AC,该二次函数图象的对称轴与x轴相交于点D.
(1)求这个二次函数的解析式、
(2)点D的坐标及直线BC的函数解析式;
(3)点Q在线段BC上,使得以点Q、D、B为顶点的三角形与△ABC相似,求出点Q的坐标;
(4)在(3)的条件下,若存在点Q,请任选一个Q点求出△BDQ外接圆圆心的坐标.
(1)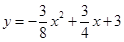 ;(2)(1,0),
;(2)(1,0), ;(3)(2,
;(3)(2,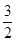 )或(
)或(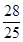 ,
,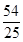 );(4)(
);(4)(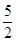 ,
,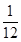 ).
).
解析试题分析:(1)设二次函数为y=a(x+2)(x﹣4),把点C(0,3)代入求出a的值即可得出二次函数的解析式;
(2)由(1)中抛物线的解析式求出对称轴方程,故可得出D点坐标,利用待定系数法求出直线BC的解析式;
(3)根据勾股定理求出BC的长,由于相似三角形的对应角不能确定,故应分∠QDB=∠CAB和∠DQB=∠CAB两种情况进行讨论;
(4)当点Q的坐标为(2,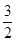 )时,设圆心的M(
)时,设圆心的M(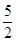 ,y),根据MD=MQ即可求出y的值,故可得出结论.
,y),根据MD=MQ即可求出y的值,故可得出结论.
试题解析:(1)∵二次函数y=ax2+bx+c的图象与x轴交于两个不同的点A(﹣2,0)、B(4,0),与y轴交于点C(0,3),
∴设二次函数为y=a(x+2)(x﹣4),把点C(0,3)代入得,a(0+2)(0﹣4)=3,解得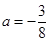 ,
,
∴这个一次函数的解析式为: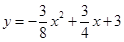 ;
;
(2)∵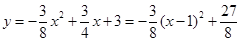 ,∴抛物线的对称轴是直线
,∴抛物线的对称轴是直线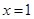 ,∴点D的坐标为(1,0).设直线BC的解析式为;
,∴点D的坐标为(1,0).设直线BC的解析式为;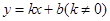 ,∴
,∴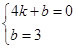 ,解得
,解得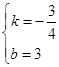 ,∴直线BC的解析式为
,∴直线BC的解析式为 .
.
(3)∵A(﹣2,0),B(4,0),C(0,3),D(1,0),∴OD=1,BD=3,CO=3,BO=4,AB=6,∴BC= ,
,
如图1,当∠QDB=∠CAB时,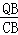 =
=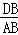 ,
,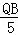 =
=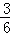 ,解得QB=
,解得QB=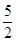 ,过点Q作QH⊥x轴于点H,∵OC⊥x轴,∴QH∥CO.∴
,过点Q作QH⊥x轴于点H,∵OC⊥x轴,∴QH∥CO.∴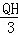 =
=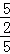 .解得QH=
.解得QH=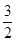 .把
.把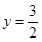 代入
代入 ,得
,得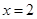 .∴此时,点Q的坐标为(2,
.∴此时,点Q的坐标为(2,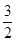 );
);
如图2,当∠DQB=∠CAB时,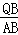 =
=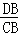 ,即
,即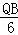 =
=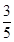 ,得QB=
,得QB=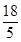 .过点Q作QG⊥x轴于点G,∵OC⊥x轴,∴QG∥CO.∴
.过点Q作QG⊥x轴于点G,∵OC⊥x轴,∴QG∥CO.∴ =
= .解得QG=
.解得QG=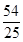 .把
.把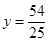 代入
代入 ,得
,得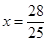 .∴此时,点Q的坐标为(
.∴此时,点Q的坐标为(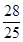 ,
,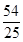 ).
).
综上所述,点Q坐标为(2,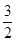 )或(
)或(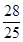 ,
,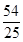 );
);
(4)当点Q的坐标为(2,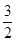 )时,设圆心的M(
)时,设圆心的M(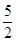 ,y).∵MD=MQ,∴
,y).∵MD=MQ,∴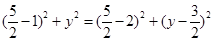 ,解得
,解得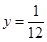 ,∴M(
,∴M(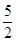 ,
,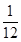 ).
).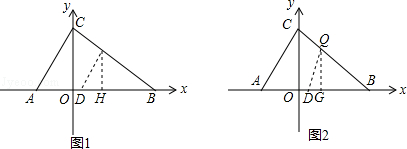
考点:二次函数综合题.


科目:初中数学 来源: 题型:解答题
某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.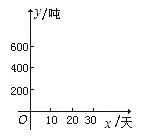
(1)分别求出甲、乙两条生产线各自总产量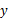 (吨)与从乙开始投产以来所用时间
(吨)与从乙开始投产以来所用时间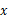 (天)之间的函数关系式.
(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案1:从包装盒加工厂直接购买,购买所需的费用y1与包装盒数x满足如图的函数关系。
方案2:租凭机器自己加工,所需费用y2(包括租凭机器的费用和生产包装盒的费用)
与包装盒数 满足如图的函数关系。
满足如图的函数关系。
根据图象回答下列问题:
(1)方案1中每个包装盒的价格是多少元?
(2)方案2中租凭机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1,y2,与x的函数表达式
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.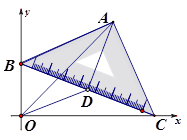
(1)取BC中点D,问OD+DA的长度是否发生改变,若会,说明理由;若不会,求出OD+DA长度;
(2)你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;
(3)填空:当OA最长时A的坐标是( , ),直线OA的解析式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校实行学案式教学,需印制若干份数学学案。印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要。两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 .
乙种收费方式的函数关系式是 .
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某生物小组观察一植物生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行x轴).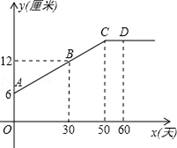
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的解析式,并求该植物最高长多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年广东梅州8分)为建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如表:
| | 单价(元/棵) | 成活率 | 植树费(元/棵) |
| A | 20 | 90% | 5 |
| B | 30 | 95% | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com