练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
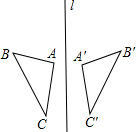
    13．如图，△ABC与△A′B′C′关于直线l对称，∠A=98°，∠C′=28°，则∠B的度数为（　　）
    A．28°B．54°C．74°D．78°

    分析 根据轴对称图形的性质可得△ABC与△A′B′C′全等，然后根据全等三角形对应角相等可得∠C=∠C′，再利用三角形内角和定理列式计算即可得解．

    解答 解：∵△ABC与△A′B′C′关于直线l对称，
    ∴△ABC≌△A′B′C′，
    ∴∠C=∠C′，
    ∵∠A=98°，∠C′=28°，
    ∴∠B=180°-∠A-∠C=180°-98°-28°=54°．
    故选B

    点评 本题考查了轴对称的性质，全等三角形的性质，三角形的内角和定理，求出∠C的度数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

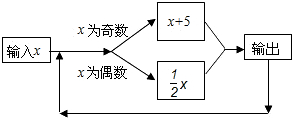    3．按如图所示的程序计算，若开始输入的x的值为48，我们发现第一次得到的结果为24，第2次得到的结果为12，…，请你探索第2013次得到的结果是（　　）
    A．2B．4C．3D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：（-$\frac{1}{3}$）-2-16÷（-2）3+（π-tan60°）0-3$\sqrt{3}$cos30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．解方程组：$\left\{\begin{array}{l}{3（y+2）=x-1}\\{5y-2（x-1）=8}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

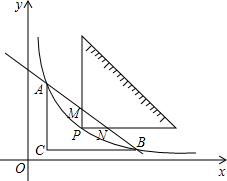    8．如图，将一块直角三角形纸板的直角顶点放在C（1，$\frac{1}{2}$）处，两直角边分别与x，y轴平行，纸板的另两个顶点A，B恰好是直线y=kx+b与双曲线y=$\frac{4}{x}$的交点．
    （1）求k和b的值；
    （2）设双曲线y=$\frac{4}{x}$在A，B之间的部分为L，让一把含45°的三角尺的直角顶点P在L上滑动，两直角边始终与坐标轴平行，且与线段AB交于M，N两点，请探究是否存在点P使得MN=$\frac{1}{2}$AB，写出你的探究过程和结论；
    （3）在（2）的条件下，△MPN 的面积是否存在最大值？若有，请求出面积最大值及点P的坐标；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列所示的图案中，有且仅有一条对称轴的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．在计数制中，通常我们使用的是“十进位制”，即“逢十进一”，而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据．已知二进位制与十进位制的比较如表：
     十进位制 0 1 2 3 4 5 6…
     二进位制 0 1 10 11 100 101 110…
    请将二进位制数1010101（2）写成十进位制数是（　　）
    A．84B．85C．170D．171

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知抛物线y=（x-1）2+2的图象上有A（$\sqrt{3}，{y}_{1}$），B（3，y2），C（-5，y3）三个点，则y1，y2，y3的大小关系是（　　）
    A．y3＞y2＞y1B．y3＞y1＞y2C．y2＞y1＞y3D．y1＞y2＞y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．先化简再求值：2x2+（2x+y）（2x-y）-（3x+y）2，其中x=1，y=3．

    查看答案和解析>>

    同步练习册答案