
【题目】如图1,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() 射线
射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转,射线
便立即逆时针回转,射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转.射线
便立即逆时针回转.射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度,射线
度,射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度.
度.

(1)直接写出![]() 的大小为_______;
的大小为_______;
(2)射线![]() 、
、![]() 转动后对应的射线分别为
转动后对应的射线分别为![]() 、
、![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,若射线
,若射线![]() 比射线
比射线![]() 先转动
先转动![]() 秒,设射线
秒,设射线![]() 转动的时间为
转动的时间为![]()
![]() 秒,求
秒,求![]() 为多少时,直线
为多少时,直线![]() 直线
直线![]() ?
?
(3)如图2,若射线![]() 、
、![]() 同时转动
同时转动![]()
![]() 秒,转动的两条射线交于点
秒,转动的两条射线交于点![]() ,作
,作![]() ,点
,点![]() 在
在![]() 上,请探究
上,请探究![]() 与
与![]() 的数量关系.
的数量关系.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
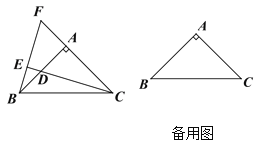
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
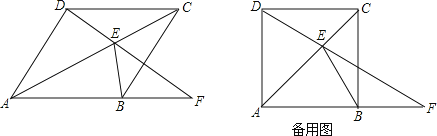
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题:
(1)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
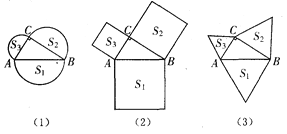
【题目】如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3。(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:如图1,△ABC中,∠B=30°,AB=3,BC=4,则△ABC的面积等于
(1)【回顾】
如图1,△ABC中,∠B=30°,AB=3,BC=4,则△ABC的面积等于 . 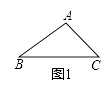
(2)【探究】
图2是同学们熟悉的一副三角尺,一个含有30°的角,较短的直角边长为a;另一个含有45°的角,直角边长为b,小明用两副这样的三角尺拼成一个平行四边形ABCD(如图3),用了两种不同的方法计算它的面积,从而推出sin75°= ![]() ,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°=
,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°= ![]() ,请你写出小明或小丽推出sin75°=
,请你写出小明或小丽推出sin75°= ![]() 的具体说理过程.
的具体说理过程.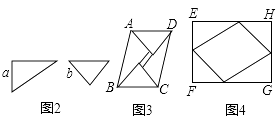
(3)【应用】
在四边形ABCD中,AD∥BC,∠D=75°,BC=6,CD=5,AD=10(如图5)
①点E在AD上,设t=BE+CE,求t2的最小值;
②点F在AB上,将△BCF沿CF翻折,点B落在AD上的点G处,点G是AD的中点吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com